Алгебра векторов, страница 12

Решение. Пусть вектор d в базисе e₁, e₂, e₃ имеет координаты x, y, z. Тогда

d  = xe₁ + ye₂ + ze₃ , т.е. i + 5j - 2k  = x(2i – k) + y(3i + 3j) + z(2i + 3k),или (2х +3у)i + (3y + 2z)j +

+ (-x +3z)k =  i + 5j - 2k. Приравнивая коэффициенты при ортах i, j, k слева и справа, получим систему уравнений:

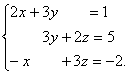
Решая систему уравнений, находим х = -4, у = 3, z = -2. Это и есть координаты вектора d в базисе e₁, e₂, e₃,  следовательно, d  = -4e₁ + 3e₂ - 2e₃.

Пример 4. Найти вектор а, коллинеарный вектору с = 3i - 6j + 2k, составляющий с осью Ох тупой угол, если |a| = 14.

            Решение. Искать вектор а будем исходя из формулы a = |a| a₀. Так как вектор a коллинеарен вектору c и образует тупой угол с осью Ох, а вектор c образует острый угол с осью Ох

(пр_i с = 3 > 0), то a₀ = - c₀. Следовательно, a = |a| (- с₀) = 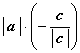. Найдем длину вектора с: , поэтому .

Пример 5. Найти вектор с, направленный по биссектрисе угла, образованного векторами

а = 2i - 2j  - k  и b = -4 i + 7j – 4 k, если .

Решение. Чтобы вектор c был направлен по биссектрисе, он должен быть диагональю ромба. Найдём модули векторов:  и   и орты  и :  и . Тогда вектор  направлен по биссектрисе. Найдем модуль вектора a₀ + b₀: 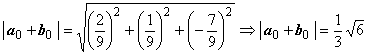 и орт . Находим вектор с = |с| (a₀ + b₀)  c = 2 i + j – 7 k.

Задачи для самостоятельной работы.

6. Найти координаты вектора 2a + b – 3c, если a = i - 2j, b = 3j – 2 k, c = i - j + k.

7. Разложить вектор d = 2 i – 6 j по векторам , , .