Алгебра векторов, страница 3

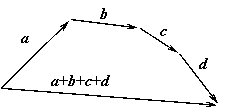
Опр. 1.1.3. Суммой n векторов a₁, a₂,  a₃, _… a_n называется вектор, соединяющий начало вектора a₁ с концом вектора a_n, если начало вектора a₂ совмещено с концом a₁, начало a₃ совмещено с концом a₂ и т.д. (рис.3).

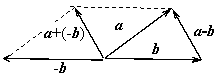Опр. 1.1.4. Разностью векторов а и b, имеющих общее начало, называется вектор, соединяющий конец вычитаемого вектора с концом уменьшаемого.

Разность векторов а и b можно найти, сложив с вектором  а противоположный вектор -b:  а - b = а + (-b).

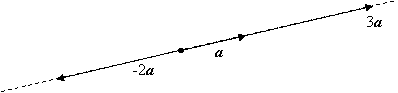Опр. 1.1.5. Произведением вектора а на в скаляр (вещественное число) называется вектор , коллинеарный вектору а, сонаправленный с ним, если  и противонаправленный к а, если , имеющий длину .

      Теорема 1.2.2. Операция умножения вектора на число обладает следующими свойствами:

1.   (ассоциативность);

2.  (дистрибутивность относительно суммы скаляров);

3.  (дистрибутивность относительно суммы векторов);

4. Для  выполняется равенство ;

5. Вектор, противоположный вектору а, получается умножением вектора а на скаляр  ();

6. При умножении  на скаляр 0 получается нулевой вектор:0.

7. Если  умножить на скаляр , то получится единичный  вектор, сонаправленный с вектором а, т.е. орт вектора а:. 

Доказательство этих утверждений также просто, как и доказательство свойств суммы векторов. Докажите их самостоятельно.

1.3. Ортогональная проекция вектора на направление (ось).

Осью будем называть прямую, на которой задано начало отсчета, направление и масштабный отрезок для измерения длин.

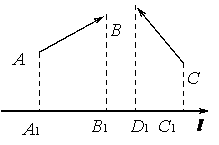
Опр. 1.3.1. Ортогональной проекцией вектора  на направление l называется число, равное длине отрезка A₁B₁, где A₁ и B₁- основания перпендикуляров, опущенных из концов вектора  на направление l, взятое со знаком плюс, если направление вектора  совпадает с направлением l и со знаком минус, если направление вектора  противоположно направлению l.