Алгебра векторов, страница 18

            1.  (или ;

            2  ;

            3. a, b, с -  правая тройка (если векторы а и b не коллинеарны).

Обозначения: [а, b], .

            Заметим, что три условия в определении векторного определения однозначно определяют результат. Первое условие определяет длину вектора с ( так как ), второе –  перпендикулярность произведения плоскости, содержащей сомножители, третье определяет нужное направление на прямой, перпендикулярной этой плоскости. Оговорка по поводу неколлинеарности сомножителей в третьем условии не сужает определение: если а и b коллинеарны, то либо по крайней мере один из этих векторов – нулевой, либо , либо ; во всех этих случаях векторное произведение дает нуль-вектор.

            1.7.2. Свойства векторного произведения:

                        1. Векторное произведение антикоммутативно, т.е. [а, b] = - [b, а];

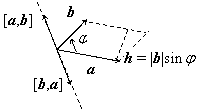                        2. [а+ b, с] = [а, с] + [b, с];

                        3. ;

4. [а, b] = 0  тогда и только тогда, когда векторы а и b коллинеарны;

5. (Геометрический смысл векторного произведения). Длина векторного произведения векторов а и b равна площади параллелограмма, построенного на этих векторах.

            Док-во: 1. При изменении порядка сомножителей плоскость, в которой лежат сомножители, остается прежней, поэтому остается прежней прямая, перпендикулярная этой плоскости, однако кратчайший поворот от первого сомножителя до второго теперь виден с другой стороны, следовательно, произведение меняет знак;

2.  Второе свойство будет доказано позже, после изучения свойств смешанного произведения;

3.  Если , то вектор [а, b] растягивается (при ) или сжимается (при ) в  раз; если , то [а, b] еще меняет и направление;

4.  [а, b] = 0, как уже говорилось, тогда и только тогда, когда либо по крайней мере один из этих векторов – нулевой, либо , либо ; во всех этих случаях векторы коллинеарны;

5.  Если на векторах а и b построить параллелограмм и рассматривать а как основание, то высота параллелограмма равна . Следствием из пятого свойства является то, что площадь треугольника, построенного на векторах а и b, равна половине длины их векторного произведения.

            1.7.3. Механический смысл векторного произведения. Если к точке А приложена сила F, то момент этой силы относительно точки О равен .