Алгебра векторов, страница 17

4. Найти проекцию вектора с = (1, 7, -5) на ось, составляющую с координатными осями равные острые углы.

5. В  заданы вершины А = (2, -2, 1), В = (2, 1, -3), С = (-3, -1, -1). Найти косинус угла ВАС.

6. Даны векторы а = i - 2 j + k, b = 3 i + k,  c = 3 j - 5 k. Найти пр_а(3b + 2c).

7. Найти координаты вектора a, коллинеарного вектору с = (1, 3, -2) и удовлетворяющего условию .

8. Параллелепипед ABCDA₁B₁C₁D₁ построен на векторах , , . Найти проекцию диагонали  на диагональ  и косинус угла между векторами  и .

9. Дан четырёхугольник ABCD с вершинами А = (1, -2, 2), В = (1, 4, 0), С = (-4, 1, 1),

D = (-5, -5, 3). Доказать ортогональность диагоналей  и .

10. Найти пр_m n, если векторы m = a - 3c, n = 5 a+ c, где |a| = 1, |c| = 2, .

11. Векторы 2a - 3c и 8a - 5c  являются диагоналями параллелограмма. Найти длины его сторон, если |a| = 2, , .

12. Найти косинус угла между векторами m и n, если векторы a = 3m - n и c = 2m + 5n взаимно ортогональны и |m| = 2, |n| = 3.

13. Найти , при котором векторы ,  ортогональны.

14. Параллелограмм ABCD построен на векторах  и . Найти проекции вектора  на диагонали  и .

15. Даны вершины А = (5, -4, 1), В = (1, -2, 3), С = (3, -1, 4) треугольника ABC. Определить внешний угол при вершине С.

16. Найти пр_с(а - 3b), если а = 5 i + 3 j, b = i - 2 k,  c = i + 2 j - 2 k.

16. Найти координаты вектора c, коллинеарного вектору a = (3, -1, 4), если с а = 13.

17. Даны точки А(4, -6, 8) и В(7, -13, 2). Найти , если а = (-1, -2, 0) и  с = (0, 3, 9).

1.7. Векторное произведение векторов.

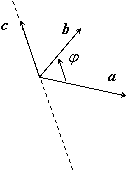            1.7.1. Определение векторного произведения векторов. Векторным произведением векторов а и b называется вектор с, длина и направление которого определяются следующими условиями: