+ аz bz(k, k) = ах bх + аy by + аz bz.
Мы доказали, что в ортонормированном базисе скалярное произведение векторов сумме попарных произведений соответствующих координат: (а, b) = ах bх + аy by + аz bz.
Теперь, зная координатное представление скалярного произведения, мы можем по новому вывести формулы для длины вектора, проекции вектора на вектор и т.д. Так, (а, а) = ах ах + аy аy + + аz аz = ах2 + аy2 + аz2, поэтому по второму свойству |a|2 = ах2 + аy2 + аz2, следовательно,
.
Из определения скалярного произведения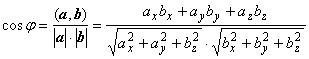 
, поэтому если векторы заданы в
координатной форме, легко находится угол между ними:
.
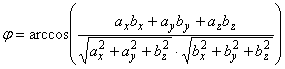Проекция вектора а на направление, определяемое вектором b, в координатной форме:
.
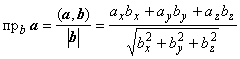В частности, если b = i = (1, 0, 0), то |b | = 1, (а, i) = (ах i + ау j + аz k, 1 i + 0 j + 0 k) = ах, и
прi a = ах. Аналогично, прj a = аy, прk a = аz, т.е. координаты любого вектора
есть проекции этого вектора на направления, заданные соответствующими ортами.
Направляющие косинусы (углов между вектором а и базисными ортами i, j, k):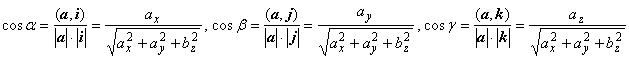 
.
Напомним, что направляющие косинусы удовлетворяют соотношению
.
Орт вектора: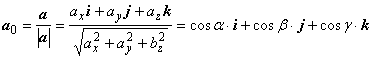 
.
Решение типовых задач.
Пример 1. Векторы d1= 4a
+ c и d2=
-2a + 5c
являются диагоналями параллелограмма. Найти длину сторон параллелограмма, если |a| = 2, |c| = 1, 
.
Решение. Пусть сторонами
параллелограмма являются векторы m и n. Используя правила сложения и вычитания векторов,
получим систему уравнений: 
,
решая которую найдём векторы m = a + 3c и n = 3a - 2c. Находим длины сторон параллелограмма по формуле:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.