Алгебра векторов, страница 20

Пример 2. Упростить выражение (a – b – с)xb + (a + b – с)xc + (a + b + с)xa.

Решение. Используя свойства векторного произведения, получим

(a – b – с)xb + (a + b – с)xc + (a + b + с)xa = axb – bxb – cxb + axc + bxc – cxc + axa + bxa + cxa =

= axb + bxc + axc + bxc – axb – axc = 2 bxc.

Пример 3. Найти координаты единичных векторов, ортогональных к плоскости ΔABC,  где  A(1, -2, 3), B(3, 0, 4), C(3, 1, 5).

Решение. Найдём координаты векторов , .Так как вектор  и , то вектор , и .

Находим единичные векторы, ортогональные к плоскости треугольника: .

Пример 4.В плоскости YOZ найти вектор с, ортогональный вектору a = (3, -2, -1), если .

Решение. По условию задачи  и  .

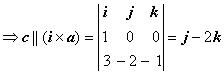Следовательно, .

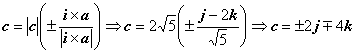Пример 5. Параллелепипед ABCDA₁B₁C₁D₁ построен на векторах , , . Вычислить площадь сечения BA₁C₁ и длину высоты Δ BA₁C₁, опущенной из вершины В на сторону A₁C₁.

Рис. 12.

Решение. Найдём векторы  и . Площадь треугольника, построенного на векторах  и , равна половине длины их векторного произведения: . Найдём векторное произведение  : . Находим . По другой формуле для вычисления площади треугольника, запишем: , где h - высота, опущенная из точки В на сторону A₁C₁. Найдём вектор  и его длину . Тогда из равенства .