Алгебра векторов, страница 14

                        4. (а + b, c) = (а, c) + (b, c);

                        5. ;

                        6. (а, 0) = 0;                                         

                        7. если , то (а, b) = 0;

8. если (а, b) = 0, то либо хотя бы один из сомножителей равен нулю, либо сомножители ортогональны.

            Док-во. Первое и второе свойства непосредственно следуют из определения: косинус – функция четная, поэтому неважно, как отсчитывается угол – от а к b  или b  к а; cos 0 = 1 (0 – угол, который образует вектор с самим собой). Докажем третье свойство: , или . Из этого свойства на основе свойств проекции легко выводятся четвертое и пятое:

(a + b, c) = |c | пр_c(a + b) = |c | (пр_ca  + пр_c b) = |c | пр_ca + |c | пр_c b = (a, c) + (b, c),

.

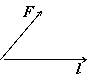            Шестое, седьмое и восьмое свойства очевидны (если b = 0, то |b| = 0; если , то ; если произведение равно нулю, то необходимо один из сомножителей, входящих в определение (|a|, либо |b|, либо ) равен нулю). Если вспомнить, что мы считаем направление нуль-вектора произвольным, то восьмое свойство можно переформулировать как необходимое и достаточное условие ортогональности векторов: два вектора ортогональны тогда и только тогда, когда их скалярное произведение равно нулю.

            Механический смысл скалярного произведения заключается в следующем. Если материальная точка под воздействием силы F перемещается на вектор l, то совершаемая этой силой работа равна скалярному произведению F  на l: A = (F, l).

            1.6.3. Скалярное произведение векторов, заданных в ортонормированном базисе.

            Пусть в ортонормированном базисе i, j, k заданы векторы а = а_х i + а_у j + а_z k и b = b_х i + b_у j + b_z k. Найдем их скалярное произведение, учитывая то, что четвертое и пятое свойства позволяют раскрывать скобки и выносить скалярные множители за знак скалярного произведения и то, что вследствие ортонормированности  (i, i) = (j, j) = (k, k) = 1, (i, j) = (j, i) = (i, k) = (k, i) = (j, k) =

= (k, j) = 0: (а, b) = (а_х i + а_у j + а_z k, b_х i + b_у j + b_z k) = а_х b_х(i, i) + а_х b_у(i, j) + … + а_z b_y(k, j) +