Алгебра векторов, страница 5

2. Достаточность. Пусть один из векторов, для определенности, а_n, есть линейная комбинация остальных, т.е. . Перепишем это равенство в виде . Мы получили нетривиальную (так как ) линейную комбинацию, равную 0, т.е. система векторов а₁, а₂, …, а_n действительно линейно зависима.

Теорема 1.4.2. Если система векторов содержит линейно зависимую подсистему, то она является линейно зависимой.

Док-во. Пусть в системе векторов а₁, а₂, …, а_n подсистема, состоящая из первых k (k<n) векторов, линейно зависима, т.е.  при нетривиальном наборе коэффициентов . Тогда , что означает линейную зависимость всей системы а₁, а₂, …, а_n, так как набор тоже нетривиален.

Теорема 1.4.3. Любая подсистема линейно независимой системы векторов является линейно независимой.

Эта теорема легко доказывается от противного на основе предыдущей теоремы.

Теорема 1.4.4. Система векторов, содержащая нулевой вектор, является линейно зависимой.

Док-во. Для системы 0, а₂, …, а_n существует нетривиальная нулевая линейная комбинация: .

Теорема 1.4.5. Система векторов, содержащая два равных или два пропорциональных вектора, является линейно зависимой.

Док-во. Пусть векторы а₁ и а₂ пропорциональны, т.е. а₂ =  (если векторы равны, то ). Если а₁ = а₂ = 0, то система а₁, а₂, …, а_n линейно зависима по предыдущей теореме. Если ,  ,  то , и имеем нетривиальную нулевую линейную комбинацию: .

Теорема 1.4.6. Два геометрических вектора линейно зависимы тогда и только тогда, когда они коллинеарны.

Док-во. Необходимость. Пусть векторы а и b линейно зависимы. Если хотя бы один из них равен нуль-вектору, то они коллинеарны (нуль-вектор коллинеарен любому другому вектору). Если оба отличны от нуль-вектора, и существует нетривиальная линейная комбинация , равная нулевому вектору, то . Из равенства , или , где . По определению, произведение  коллинеарно вектору а.

Достаточность. Пусть векторы а и b коллинеарны. Если один из них, например, а, нулевой, то нетривиальная линейная комбинация, дающая нуль-вектор, очевидна: . Если оба вектора отличны от нуль-вектора, то для равнонаправленных векторов 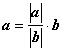, для противонаправленных 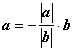, т.е. вектор а линейно выражается через b, что означает линейную зависимость пары векторов а и b.