Алгебра векторов, страница 11

Опр. 1.5.6. Направляющими косинусами вектора а назовём косинусы тех углов , которые этот вектор образует с базисными векторами, соответственно, i, j, k.

            Направляющие косинусы вектора а = (х, у, z) находятся по формулам:

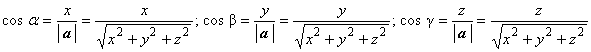                        .                Сумма квадратов направляющих косинусов равна единице:

                        .                                                                                            

Направляющие косинусы вектора a являются координатами его орта: .                                  

            1.5.4. Декартова прямоугольная система координат.

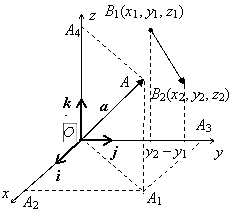
Пусть базисные орты i, j, k отложены из общей точки О. Будем считать, что орты задают положительные направления осей Ох, Оу, Oz. Совокупность точки О (начала координат) и ортонормированного базиса i, j, k называется декартовой прямоугольной системой координат в пространстве. Пусть А – произвольная точка пространства. Вектор а = ОА = xi + yj + zk называется радиусом-вектором точки А, координаты этого вектора (x, y, z) называются также координатами точки А ( обозначение: А(x, y, z)). Оси координат Ох, Оу, Oz называют также, соответственно, осью абсцисс, осью ординат, осью аппликат.

Если вектор  задан координатами своей начальной точки В₁(x₁, y₁, z₁) и конечной точки В₂(x₂, y₂, z₂), то координаты вектора  равны разности координат конца и начала:  (так как ).

Декартовы прямоугольные системы координат на плоскости и на прямой определяются совершенно аналогично с соответствующими количественными (в соответствии с размерностью) изменениями.

Решение типовых задач.

Пример 1. Найти длину и направляющие косинусы вектора  а = 6i – 2j -3k.

Решение. Длину вектора: . Направляющие косинусы: .

Пример 2. Найти координаты вектора а, образующего с координатными осями равные острые углы, если длина этого вектора равна .

Решение. Так как , то подставляя  в формулу (1.6), получим . Вектор а образует с координатными осями острые углы, поэтому орт . Следовательно, находим координаты вектора .

Пример 3. Заданы три некомпланарных вектора  e₁ = 2i – k, e₂ = 3i + 3j, e₃ = 2i + 3k. Разложить вектор d = i + 5j - 2k по базису e₁, e₂, e₃.