Алгебра векторов, страница 7

            Решение. В   вектор , но вектор .  Вектор  Вектор  принадлежит биссектрисе , так как является диагональю ромба, построенного на ортах  и . Следовательно, вектор . Но вектор . Из условия коллинеарности этих векторов  находим 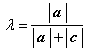, тогда вектор .

C

C1

Пример 1.4. Параллелепипед ABCDA₁B₁C₁D₁ построен на векторах , , . Выразить через них векторы  и , где точка Р делит ребро A₁B₁ в соотношении 2:1.

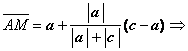
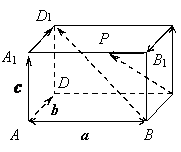
Решение. Вектор   находим как сумму векторов ,  и , тогда .

Вектор  находим как сумму векторов ,  и , тогда .

Задачи для самостоятельной работы.

1. Даны векторы а и b. Построить векторы .

2. В правильном шестиугольнике ABCDEF векторы , . Выразить через p и q векторы .

3.  построен на векторах , . Выразить через a, b медианы треугольника.

4.  построен на векторах , .Найти вектор произвольной длины, коллинеарный биссектрисе угла .