Следствие. Если два вектора линейно зависимы, то один из них линейно выражается через другой.
Теорема 1.4.7. Три геометрических вектора линейно зависимы тогда и только тогда, когда они компланарны.
Следствие. Если векторы а
и b неколлинеарны,
и вектор с компланарен с векторами а и b, то с линейно выражается через
векторы а и b (с
является линейной комбинацией а и b),
т.е. существуют коэффициенты ![]() и
и ![]() такие, что
такие, что ![]() .
.
Теорема 1.4.8. Любые четыре геометрических вектора всегда линейно зависимы.
Следствие. Если векторы а,
b и с
некомпларны, то любой другой вектор d
линейно выражается через векторы а, b
и с (является их линейной комбинацией), т.е. существуют
коэффициенты ![]() ,
, ![]() и
и
![]() такие, что
такие, что ![]() .
.
Теоремы 1.4.7 и 1.4.8 доказать самостоятельно.
Решение типовых задач.
 Пример 1.1. В
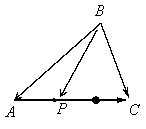
Пример 1.1. В ![]() , построенном на векторах
, построенном на векторах ![]() и
и ![]() ,
сторону АС разделили точками Р и М на три равные части.
Найти вектор
,
сторону АС разделили точками Р и М на три равные части.
Найти вектор ![]() .
.
Решение. В ![]() находим вектор
находим вектор ![]() , но вектор
, но вектор ![]() .
В
.
В ![]() находим вектор
находим вектор ![]() с – а и
с – а и
![]() . Тогда вектор
. Тогда вектор ![]() .
.
 Пример 1.2. Вравнобедренной трапеции ABCD боковая сторона
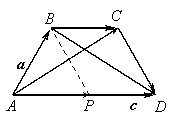
Пример 1.2. Вравнобедренной трапеции ABCD боковая сторона ![]() , нижнее основание
, нижнее основание ![]() ,
, ![]() .
Найти стороны
.
Найти стороны ![]() и
и ![]() и
диагонали
и
диагонали ![]() и
и ![]() трапеции.
трапеции.
 Решение. Вравнобедренной трапеции ABCD строим BP||CD, тогда
Решение. Вравнобедренной трапеции ABCD строим BP||CD, тогда ![]() - равносторонний
и вектор
- равносторонний
и вектор ![]() |a|c0
|a|c0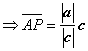 .
Вектор
.
Вектор ![]()
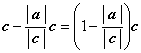 .
Вектор
.
Вектор ![]() с – а.
Вектор
с – а.
Вектор ![]()
![]()
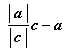 . Вектор
. Вектор ![]()
![]()
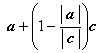 .
.
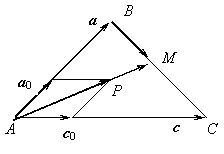
Пример 1.3. ![]() построен на векторах
построен на векторах ![]() ,
, ![]() .
Найти вектор
.
Найти вектор ![]() , коллинеарный биссектрисе
, коллинеарный биссектрисе ![]() ,если точка М лежит на стороне
ВС.
,если точка М лежит на стороне
ВС.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.