2. Аналитическая геометрия на плоскости и в пространстве.
Повторим определения раздела 1.5.4.
2.1.1. Декартова прямоугольная система координат.
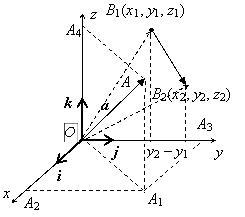 Совокупность точки О (начала координат)
и ортонормированного базиса i, j, k, векторы
которого отложены из точки О, называется декартовой прямоугольной
системой координат в пространстве. Прямые Ох, Оу, Oz, проходящие через точку О в направлении
базисных ортов, называются осями координат (осью абсцисс, осью ординат,
осью аппликат). Пусть А – произвольная точка пространства. Вектор
rA
= ОА = xi + yj + zk называется радиусом-вектором
точки А, координаты этого вектора (x,
y, z) (равные
проекциям вектора на координатные оси) называются также координатами точки А
(обозначение: А(x, y,
z)).
Совокупность точки О (начала координат)
и ортонормированного базиса i, j, k, векторы
которого отложены из точки О, называется декартовой прямоугольной
системой координат в пространстве. Прямые Ох, Оу, Oz, проходящие через точку О в направлении
базисных ортов, называются осями координат (осью абсцисс, осью ординат,
осью аппликат). Пусть А – произвольная точка пространства. Вектор
rA
= ОА = xi + yj + zk называется радиусом-вектором
точки А, координаты этого вектора (x,
y, z) (равные
проекциям вектора на координатные оси) называются также координатами точки А
(обозначение: А(x, y,
z)).
 Если вектор
Если вектор ![]() задан координатами своей начальной
точки В1(x1, y1, z1)
и конечной точки В2(x2,
y2, z2),
то координаты вектора
задан координатами своей начальной
точки В1(x1, y1, z1)
и конечной точки В2(x2,
y2, z2),
то координаты вектора ![]() равны разности
координат конца и начала:
равны разности
координат конца и начала: ![]() (так как
(так как ![]() ).
).
В дальнейшем нам придется сдвигать систему координат на определенный вектор. Выясним, как при этом меняются координаты точек и векторов.
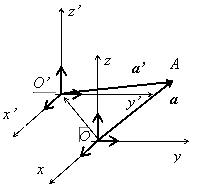
Параллельный перенос координат. Пусть
новая система координат (O’, x’, y’, z’) получена из старой (O,
x, y, z) сдвигом на вектор ![]() .
Тогда
.
Тогда ![]()
![]() . Базисные орты в обеих
системах одинаковы, поэтому координаты вектора
. Базисные орты в обеих
системах одинаковы, поэтому координаты вектора ![]() есть
координаты точки О’ в новой системе координат:
есть
координаты точки О’ в новой системе координат: 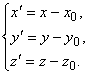
2.1.2. Простейшие задачи аналитической геометрии.
2.1.2.1. Расстояние между двумя точками (длина отрезка). Эту задачу мы уже рассматривали. Длина отрезка В1В2 (верхний рисунок) равна длине вектора, соединяющего эти точки, т.е.
![]() .
.
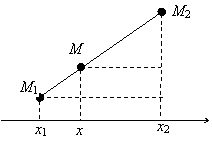
2.1.2.2. Деление отрезка в
данном отношении. Говорят, что точка М делит отрезок М1М2
в отношении ![]() , если
, если ![]() . Найдем координаты точки М.
На рисунке справа изображен отрезок и его проекция на ось Ох. Из подобия
треугольников
. Найдем координаты точки М.
На рисунке справа изображен отрезок и его проекция на ось Ох. Из подобия
треугольников 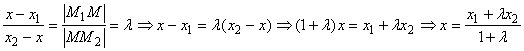 . Так же можно получить
выражения для координат у, z.
Окончательно, координаты точки, делящей отрезок в отношении
. Так же можно получить
выражения для координат у, z.
Окончательно, координаты точки, делящей отрезок в отношении ![]() , равны
, равны ![]() В
частном случае
В
частном случае ![]() , т.е. когда точка М
– середина отрезка, получаем, что координаты середины отрезка равны средним
арифметическим координат концов:
, т.е. когда точка М
– середина отрезка, получаем, что координаты середины отрезка равны средним
арифметическим координат концов: ![]()
2.1.2.3. Площадь
треугольника. Пусть в пространстве треугольник задан координатами своих
вершин: А(x1, y1, z1),
B(x2, y2, z2),C(x3,
y3, z3).
Тогда ![]() ,
, ![]() ,
и площадь тр-ка ABC равна
половине площади параллелограмма, построенного на этих векторах:
,
и площадь тр-ка ABC равна
половине площади параллелограмма, построенного на этих векторах: 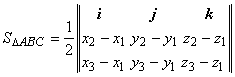 . Если треугольник лежит в плоскости Оху,
то z1 = z2
= z3 = 0, то, раскрывая определитель
по третьему столбцу, получим
. Если треугольник лежит в плоскости Оху,
то z1 = z2
= z3 = 0, то, раскрывая определитель
по третьему столбцу, получим 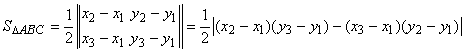 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.