Аналитическая геометрия на плоскости и в пространстве, страница 10

            2.1.5.2. Пучок плоскостей. Уравнение пучка плоскостей. Пучком плоскостей называется множество плоскостей, проходящих через данную прямую l. Если прямая задана своим общим уравнением 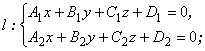то уравнение любой плоскости пучка может быть получено в виде линейной комбинации уравнений плоскостей, определяющей прямую, т.е. в виде  при подходящих значениях коэффициентов и . Уравнение  при всевозможных неравных одновременно нулю значениях и  называется уравнением пучка плоскостей.

            Пример: найти уравнение плоскости, проходящей через прямую  и проходящую через точку .

            Решение: искомая площадь принадлежит пучку плоскостей, проходящих через прямую l, поэтому ее уравнение имеет вид  при подходящих значениях и . Эта плоскость проходит через точку А, поэтому координаты точки должны удовлетворять уравнению: , или . Это равенство верно, если , , поэтому искомое уравнение имеет вид , или .

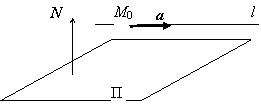            2.1.5.3. Взаимное расположение прямой и плоскости. Прямая l может быть параллельна плоскости (в частности, лежать в плоскости) и пересекаться с ней. Будем считать, что плоскость П задана своим общим уравнением

Ах + Ву + Сz + D = 0, прямая l – точкой M₀(х₀, у₀, z₀)и направляющим вектором а(m, n, p).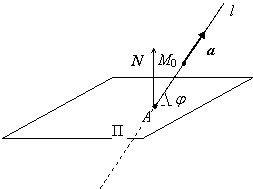  l параллельна П тогда и только тогда, когда Na, поэтому условие параллельности прямой и плоскости состоит в том, что Аm + Вn + Сp + D = 0. Если, дополнительно, , т.е. выполняется Ах₀ + Ву₀ + Сz₀ + D = 0, то прямая лежит в плоскости.

            Если Аm + Вn + Сp + D 0, то прямая и плоскость пересекаются. Для нахождения точки пересечения подставим параметрические выражения для х, у, z 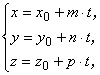 в уравнение плоскости: А(х₀ + mt) + В(y₀ + nt) + С(z₀ + pt) + D = 0 и найти значение параметра t, соответствующее точки пересечения: ; параметрические выражения для х, у, z при этом значении t  дают координаты точки пересечения.

            Угол  между прямой и плоскостью (т.е. угол между прямой и ее проекцией на плоскость) связан с углом  между прямой и нормалью к плоскости соотношением , поэтому 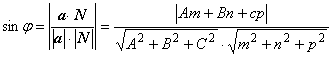. В частности, если векторы а и N коллинеарны, то прямая перпендикулярна плоскости.