Аналитическая геометрия на плоскости и в пространстве, страница 8

.

            Пример 7. Найти косинус угла между плоскостями 5х - y + 3z - 2 = 0 и 2х + 6y – 5z + 1 = 0.

            Решение. Находим векторы нормалей ,  к заданным плоскостям. .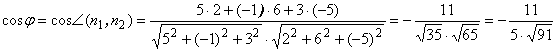

Если требуется найти острый угол между плоскостями, то.

Задачи для самостоятельной работы.

1. Составить уравнение плоскости, перпендикулярной вектору  и проходящий через точку С, если А(-3, 5, -4), С(-1, 0, -1).

2. Составить уравнение плоскости, проходящей через точку Р(0, 1, 3) параллельно

плоскости 7х – y – 3z + 4 = 0.

3. Составить уравнение плоскости, проходящей через точку А(2, 1, -3) параллельно векторам

а(2, 1, 0) и с(-1, -3, 2).

4. Составить уравнение плоскости, проходящей через точки Р₁(1, 3, 1) и Р₂(2, 1, 4) перпендикулярно к плоскости 4х – 7y – 3z + 5 = 0.

5. Составить уравнение плоскости, проходящей через ось Oz и точку С(4, 6, -1).

6. Найти косинус угла между плоскостями 2х + 2y + z + 9 = 0 и 3х – 2y – 2z - 19 = 0.

7. Найти расстояние от точки Р(2, 0, -1) до плоскости 3y – 4z + 11 = 0.

8. Найти расстояние между параллельными плоскостями 3х–2y – z - 13=0  и 6х–4y – 2z + 15= 0.

9. Найти величины отрезков, отсекаемых на координатных осях плоскостью 2х–5y + 3z - 30 = 0.

10. Составить уравнение плоскости, проходящей через точки Р₁(3, -2, 5) и Р₂(1, -3, 4) параллельно вектору .

11. Составить уравнение плоскости, проходящей через три точки Р₁(1, 5, 6), Р₂(2, 3, 1) ,

Р₃(3, -1, 2).

12. Составить уравнение плоскости, проходящей через точку А(-1, 2, 0) перпендикулярно плоскостям х – y + 3z - 4 = 0 и 2х + y – 5z + 7 = 0.

13. Составить уравнение плоскости, проходящей через точки Р₁(2, -3, 3) и Р₂(4, -2, 5) и отсекающей на оси аппликат отрезок с = 2.

14. Найти косинус угла между плоскостями 4х + 2y – z – 7 = 0 и 6х + 3z + 5 = 0.

15. Найти расстояние между параллельными плоскостями 2х – y + z – 10 = 0 и

4х – 2y + 2z – 15 = 0.

16. Вычислить расстояние от точки А(2, -1, 1) до плоскости, отсекающей от осей координат отрезки а = 2, b = -3, c = 1.

2.1.6. Прямая в пространстве.

2.1.5.1. Определение прямой. Векторное уравнение прямой. Параметрические и канонические уравнения прямой. Пусть в пространстве задан ненулевой вектор a(m, n, p) и точка М₀(x₀, y₀, z₀). Прямой, проходящей через точку М₀ в направлении вектора а называется геометрическое место точек М (x, y, z) пространства таких, что вектор коллинеарен вектору а.

Так как а ≠ 0, условие коллинеарности векторов и а имеет вид . Если r_М0 – радиус-вектор точки М₀, r_М – радиус-вектор точки М, то для любой точки М прямой выполняется , или