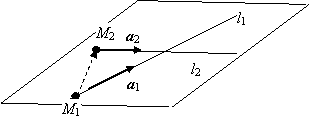Аналитическая геометрия на плоскости и в пространстве, страница 11

2.1.5.3. Взаимное расположение двух прямых. Две прямые могут быть компланарными (это означает, что существует плоскость, содержащая обе прямые) или скрещиваться (плоскости, содержащей обе прямые, не существует). В случае компланарности прямые могут совпадать, быть параллельными или пересекаться. Найдем условия, когда реализуется каждый из перечисленных случаев. Будем считать, что прямая l₁ задана своей точкой M₁(х₁, у₁, z₁) и направляющим вектором а₁(m₁, n₁, p₁), прямая l₂ задана своей точкой M₂(х₂, у₂, z₂) и направляющим вектором а₂(m₂, n, p₂).

            Прямые компланарны тогда, и только тогда, когда компланарны векторы а₁, а₂ и М₁М₂. Таким образом, условие компланарности имеет вид

            .

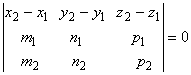            Если при этом векторы а₁и а₂ коллинеарны, т.е. , то прямые параллельны. Если, дополнительно, вектор М₁М₂ коллинеарен направляющим векторам, то прямые совпадают. 

Если условие компланарности выполняется, но направляющие векторы неколлинеарны, то прямые пересекаются. Чтобы найти точку пересечения, надо решить систему уравнений

Если условие компланарности не выполняются, то прямые скрещиваются. Вектор, перпендикулярный одновременно и l₁, и l₂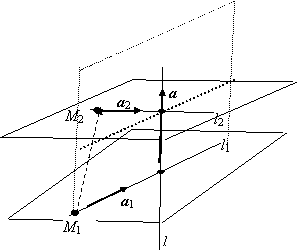, находится как векторное произведение направляющих векторов а₁ и а₂: а = а₁ха₂. Расстояние между l₁ и l₂ находится как проекция вектора М₁М₂ на а: 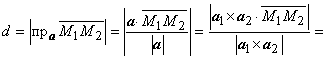 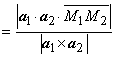. В этом соотношении легко увидеть формулу для вычисления высоты параллелепипеда как частного объема и площади основания. Далее, для плоскости, содержащей l₁ и параллельной l₂, известна точка (М₁) и нормальный вектор (а), аналогично можно выписать уравнение плоскости, содержащей l₂ и параллельной l₁. Для того, чтобы найти уравнения прямой, перпендикулярной одновременно и l₁, и l₂, необходимо найти точку этой прямой (направляющий вектор этой прямой – вектор а). Для этого можно найти пересечение прямой l₂ с плоскостью, проходящей через l₁ и параллельной вектору а (уравнение этой плоскости записывается как условие компланарности векторов М₁М, а₁ и а, где М(х, у, z) – текущая точка этой плоскости).

Решение типовых задач.