Аналитическая геометрия на плоскости и в пространстве, страница 3

            Рассмотрим две несовпадающие точки (х₁, у₁) и (х₂, у₂), принадлежащие прямой. Вычитая равенство у₁ = к х₁ + b из равенства у₂ = к х₂ + b, получим у₂ – у₁ = к (х₂ – х₁), откуда  . Но из рисунка следует, что . Таким образом, параметр к, который называют угловым коэффициентом прямой, равен тангенсу угла наклона прямой: . Положив х = 0 в уравнении у = к х + b х, получим у = b. Таким образом, параметр b равен ординате точки пересечения прямой с осью Оу.

            Так , уравнение с угловым коэффициентом невозможно записать для прямых с , т.е. для прямых, параллельных оси Оу. Такие прямые имеют уравнение х = х₀, где х₀ – абсцисса точки пересечения прямой с осью Ох.

            2.1.4.3. Общее уравнение прямой. Вернемся к векторному уравнению прямой . Запишем скалярное произведение в координатной форме: N = (A, B), , следовательно, А(х – х₀) + В(у – у₀) = 0. Преобразуем это уравнение:

Ах + Ву + (–Ах₀ – Ву₀) = 0. Обозначим С = –Ах₀ – Ву₀, тогда A x + B y + C = 0, это уравнение называется общим уравнением прямой. Итак, общим уравнением прямой называется уравнение вида

A x + B y + C = 0.

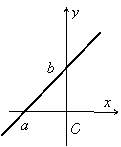Уравнение с угловым коэффициентом у = к х + b является частным случаем общего уравнения (к х - у - b = 0, А = к, В = -1, С = - b). Уравнение х = х₀ прямой, параллельной оси Оу, которую нельзя описать уравнением с угловым коэффициентом, также является частным случаем общего уравнения (х – х₀ = 0, А = 1, В = 0, С = - х₀). Справедливо и обратное утверждение: каждое общее уравнение прямой A x + B y + C = 0 может быть приведено либо к уравнению с угловым коэффициентом (если , то, решив уравнение относительно у, получим ,  ) , либо к виду х = х₀ (если В = 0, то ,  и .)

            2.1.4.4. Уравнение прямой в отрезках. Так называется уравнение вида . Положив в этом уравнении х = 0,  получим y = b; при у  = 0 получаем х = а. Таким образом, параметры а и b равны, соответственно, абсциссе и ординате концов отрезков, отсекаемых прямой на осях Ох и Оу. В отрезках может быть записана любая прямая, не проходящая через начало координат. Общее уравнение A x + B y + C = 0 приводится к уравнению в отрезках при  делением на –С: , т.е. .