2.1.4.5. Частные случаи общего уравнение прямой A x + B y + C = 0.
Если А = 0, то ![]() ,
и уравнение приводится к виду
,
и уравнение приводится к виду ![]() . Прямая
параллельна оси Ох.
. Прямая
параллельна оси Ох.
Если В = 0, то ![]() , и уравнение приводится к виду
, и уравнение приводится к виду ![]() . Прямая параллельна оси Оу.
. Прямая параллельна оси Оу.
Если С = 0, то точка О(0, 0) удовлетворяет уравнению прямой. Прямая проходит через начало координат.
2.1.4.6. Угол между прямыми. Условия параллельности и перпендикулярности прямых. Пусть прямая l1 задана уравнением
у = к1х + b1, прямая l2
задана уравнением у = к2х + b2; ![]() . Обозначим
. Обозначим ![]() угол между этими прямыми. Так как
угол между этими прямыми. Так как ![]() , то
, то ![]() .
Таким образом,
.
Таким образом, 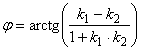 . Если прямые заданы своими
общими уравнениями
. Если прямые заданы своими
общими уравнениями
l1 : A1x + B1y + C1
= 0, l2 : A2x + B2y
+ C2 = 0, то ![]() ,
и
,
и 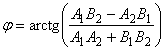 .
.
Отсюда выводятся условие
параллельности прямых: l1|| l2, если к1 = к2,
или ![]() , или А1В2
= А2В1.
, или А1В2
= А2В1.
и условие перпендикулярности прямых: ![]() , или
, или
А1А2 + В1В2 = 0.
2.1.4.7. Условие перпендикулярности вектора и
прямой. Любой вектор, перпендикулярный прямой, называется нормальным
(к этой прямой). Если прямая l задана
своим общим уравнением A x + B y + C
= 0, то вектор N(A,
B) нормален к l. Любой
другой ненулевой вектор р(a, b), нормальный к прямой l,
должен быть коллинеарным вектору N(A,B), поэтому окончательно
условие перпендикулярности вектора и прямой запишется в виде ![]() .
.
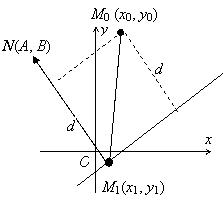 2.1.4.7. Расстояние от точки до прямой. Пусть
прямая l задана уравнением A x + B y
+ C = 0, M0(x0, y0)
– произвольная точка плоскости. Для любой точки М1(x1, y1),
лежащей на прямой, расстояние d от точки M0 до прямой l
равно абсолютной величине проекции вектора
2.1.4.7. Расстояние от точки до прямой. Пусть
прямая l задана уравнением A x + B y
+ C = 0, M0(x0, y0)
– произвольная точка плоскости. Для любой точки М1(x1, y1),
лежащей на прямой, расстояние d от точки M0 до прямой l
равно абсолютной величине проекции вектора ![]() на
нормальный вектор N(A,
B). Пусть точка М1 имеет
координаты (x1, y1),
тогда
на
нормальный вектор N(A,
B). Пусть точка М1 имеет
координаты (x1, y1),
тогда![]() , и
, и
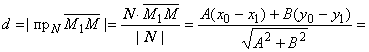
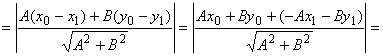
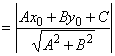 ,
так как из принадлежности точки М1 прямой l следует, что Ax1 + By1
+ C = 0, т.е. (-Ax1 - By1)
= С. Таким образом, чтобы найти расстояние от точки до прямой,
достаточно подставить координаты точки в общее уравнение прямой и полученное
число разделить на длину нормального вектора. Так, расстояние между точкой M(1, 2) и прямой 3х + 4у + 5 = 0 равно
,
так как из принадлежности точки М1 прямой l следует, что Ax1 + By1
+ C = 0, т.е. (-Ax1 - By1)
= С. Таким образом, чтобы найти расстояние от точки до прямой,
достаточно подставить координаты точки в общее уравнение прямой и полученное
число разделить на длину нормального вектора. Так, расстояние между точкой M(1, 2) и прямой 3х + 4у + 5 = 0 равно  . Расстояние от этой прямой до точки M(-5; 2,5) равно
. Расстояние от этой прямой до точки M(-5; 2,5) равно 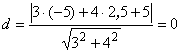 ,
т.е. эта точка лежит на прямой.
,
т.е. эта точка лежит на прямой.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.