Аналитическая геометрия на плоскости и в пространстве, страница 13

Расстояние между скрещивающимися прямыми равно расстоянию между параллельными плоскостями, проведёнными через данные прямые. Вектор нормали n этих плоскостей перпендикулярен векторам a₁ и a₂, следовательно . Находим 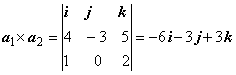, следовательно n = -2i – j + k. Находим расстояние  между прямыми.

Задачи для самостоятельной работы.

1. Составить канонические и общие уравнения прямой, проходящей через точку Р(2, 3, -4) параллельно вектору a(-4, 0, 7).

2. Составить канонические и общие уравнения прямой, проходящей через точку Р(6, 2, -3) параллельно прямой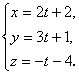

3. Составить канонические и параметрические уравнения прямых, проходящих через точку

A(2, -3, 0), если направляющие вектора прямых образуют с координатными осями Ox и Oy углы .

4. Составить канонические, параметрические и общие уравнения прямой, проходящей через точки A(5, 7, -3) и B(2, 5, 0).

5. Привести к каноническому виду общие уравнения прямой

6. В плоскости Oxу найти прямую, проходящую через точку A(4, -5, -7) перпендикулярно прямой .

7. Определить острый угол между прямым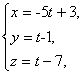и  и .

8. Проверить, пересекаются ли прямые  и .

9. Составить параметрические уравнения прямой, проходящей через точки A(4, -3, 8) и

C(6, 2, 5).

10. Привести к каноническому виду общие уравнения прямой

11. Составить канонические и параметрические уравнения прямой, проходящей через точку A(2, -1, 9) параллельно прямой

10. Доказать параллельность прямых 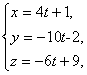 и

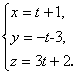11. Проверить, скрещиваются ли прямые  и . Найти расстояние между ними.

12. Доказать перпендикулярность прямых  и

13. Определить косинус угла между прямыми 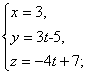 и