Аналитическая геометрия на плоскости и в пространстве, страница 2

2.1.3. Основные задачи аналитической геометрии.

            2.1.3.1. Геометрический смысл уравнений f(x, y) = 0  и F(x, y, z) =0.

            Уравнение  f(x, y) = 0 называется уравнением линии l на плоскости, если этому уравнению удовлетворяют координаты х, у всех точек М(х, у), лежащих на линии, и не удовлетворяют координаты ни одной точки P(х, у), не лежащей на кривой:

            f(x, y) = 0  М(х, у) l,

            f(x, y)  0  М(х, у) l.

            Уравнение  F(x, y, z) = 0 называется уравнением поверхности  в пространстве, если этому уравнению удовлетворяют координаты х, y, z всех точек М(х, у, z), лежащих на поверхности, и не удовлетворяют координаты ни одной точки P(х, у, z), не лежащей на поверхности:

            F(x, y, z) = 0  М(х, у, z) ,

            F(x, y, z)  0  М(х, у, z) .

            2.1.3.1. Две основные задачи аналитической геометрии.

            Задача 1. Дано некоторое множество точек плоскости (пространства), обладающее некоторым набором свойств. Требуется составить уравнение (или систему уравнений), которое в некоторой системе координат задает это множество точек.

            Задача 2 (обратная). В заданной системе координат некоторое множество точек плоскости (пространства) описывается заданным уравнением (или системой уравнений). Требуется определить вид и основные свойства этого множества и построить его эскиз.

2.1.4. Прямая на плоскости.

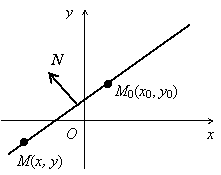            2.1.4.1. Векторное уравнение прямой. Пусть на плоскости задана точка М₀(x₀, у₀) и ненулевой вектор N(A, B). В аналитической геометрии прямая задается как геометрическое место точек М(x, у) таких, что вектор  ортогонален вектору N.  Таким образом, в векторном виде уравнение прямой записывается так:

                        .

(скалярное произведение ортогональных векторов равно нулю).

Дальше мы вернемся к этому уравнению; сначала вспомним, что известно о прямой из школы.

2.1.4.2. Уравнение прямой с угловым коэффициентом.  

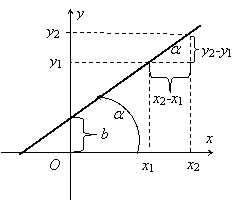
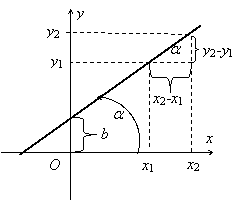Уравнением прямой с угловым коэффициентом называется уравнение вида  у = к х + b. Выясним смысл параметров к и b.

Углом наклона прямой называется любой направленный угол, на который надо повернуть ось Ох, чтобы получить одно из направлений прямой. Очевидно, все углы наклона прямой отличаются друг от друга на величину , поэтому их тангенсы равны.