Аналитическая геометрия на плоскости и в пространстве, страница 7

            Пример 2. Составить уравнение плоскости, проходящей через точки А(4, 1, -3), В(7, -1, 2) параллельно оси Oy.

            Решение. Пусть переменная точка Р(x, y, z) принадлежит данной плоскости. Решим задачу двумя способами.

            I способ. Вектор  принадлежит плоскости. Находим координаты вектора  и орта j(0, 1, 0). Вектор нормали к плоскости находим по формуле:

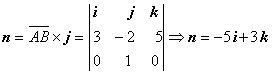            . Тогда уравнение плоскости имеет вид

-5(х – 4) + 3(z + 3) = 0, или 5х – 3z – 29 = 0.

            II способ. Векторы ,  и орт j(0, 1, 0) компланарны, следовательно, их смешанное произведение равно нулю. Запишем в векторной форме уравнение плоскости: . Тогда в координатной форме уравнение плоскости имеет вид:

.

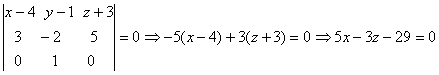            Пример 3. Составить уравнение плоскости, проходящей через точку Р₁(5, -2, 0) перпендикулярно к плоскостям 7х – 2y – 5 = 0 и 5х – 2y – z – 7 = 0.

            Решение. Пусть текущая точка Р(x, y, z) принадлежит искомой плоскости. Вектор  и векторы нормалей n₁(7, -2, 0) и n₂(5, -2, 1) заданных плоскостей компланарны, следовательно их смешанное произведение равно нулю:

.

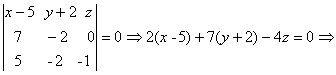
            Пример 4. Составить уравнение плоскости, проходящей через точки Р₁(-1, 3, 2), Р₂(1, 3, 1) перпендикулярно к плоскости 5х + 3y – 2z – 9 = 0.

            Решение. Пусть переменная точка Р(x, y, z) принадлежит искомой плоскости. Векторы ,  и  (вектор нормали заданной плоскости) компланарны. Записывая условие компланарности этих векторов, получим в векторной форме уранение плоскости: . Запишем в координатной форме уравнение плоскости:

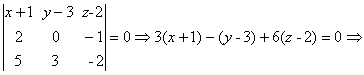3х – y + 6z – 6 = 0.

            Пример 5. Найти расстояние от точки Р₀(2, -1, -2) до плоскости, проходящей через точки Р₁(2, 1, -3), Р₂(5, -1, -2), Р₃(1, 2, -1).

            Решение. Пусть Р(x, y, z) - текущая точка искомой плоскости. Векторы , ,  компланарны. Уравнение плоскости:

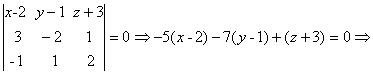   5х + 7y – z – 20 = 0.

            Расстояние от точки Р₀(2, -1, -2) до плоскости 5х + 7y – z – 20 = 0:

            .

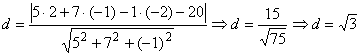            Пример 6. Убедиться, что плоскости 6х + 4y – 10z – 18 = 0 и 3х + 2y – 5z + 10 = 0 параллельны и найти расстояние между ними.

            Решение. Заданные плоскости параллельны, т.к. . Находим на плоскости 6х + 4y – 10z – 18 = 0 точку, положив у = 0, z = 0, тогда 6х – 18 = 0, откуда х = 3. Найдём расстояние от точки Р₀(3, 0, 0) до плоскости 3х + 2y – 5z + 10 = 0: