Аналитическая геометрия на плоскости и в пространстве, страница 6

Плоскости перпендикулярны тогда и только тогда, когда ортогональны их нормальные векторы, т.е.условие перпендикулярности прямых имеет вид .

Так, уравнения 2x + 3y – 4z + 5 = 0 и –6x – 9y + 12z – 15 = 0 задают одну и ту же плоскость; уравнения 2x + 3y – 4z + 5 = 0 и –6x – 9y + 12z + 1 = 0 задают параллельные плоскости; уравнения 2x + 3y – 4z + 5 = 0 и –6x + 4y – 15 = 0 задают перпендикулярные плоскости.

            2.1.5.4. Расстояние от точки до плоскости. Пусть плоскость П задана уравнением

A x + B y + C + D = 0, M₀(x₀, y_0, z₀) – произвольная точка пространства. Для любой точки М₁(x₁, y₁, z₁), лежащей на плоскости, расстояние d от точки M₀ до плоскости П равно абсолютной величине проекции вектора  на нормальный вектор N(A, B, С). Пусть точка М₁ имеет координаты (x₁, y_1, z₁), тогда, и

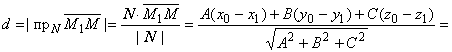
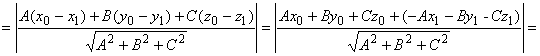
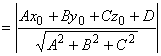 , так как из принадлежности точки М₁ плоскости П следует, что Ax₁ + By₁ + Cz₁ + D = 0, т.е. (-Ax₁ - By₁ - Cz₁) = D.

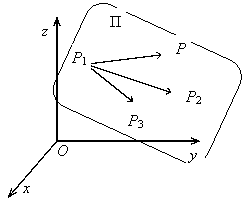            2.1.5.5. Плоскость, проходящая через три данные точки. Даны три точки М₁(x₁, y₁, z₁), М₂(x₂, y₂, z₂), М₃(x₃, y₃, z₃),  не лежащие на одной прямой (т.е. векторы  и  не коллинеарны). Введем в задачу точку М(x, y, z) – текущую точку плоскости. Векторы ,  и  лежат в одной плоскости, т.е. компланарны, следовательно, их смешанное произведение равно нулю: , или, в координатной форме, .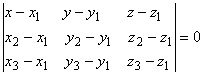

2.1.5.6. Уравнение плоскости в отрезках – это уравнение вида . Параметры а, b и с равны, соответственно, абсциссе, ординате и аппликате концов отрезков, отсекаемых прямой на осях Ох, Оу и Oz. Общее уравнение Ах + Ву + Сz + D = 0 приводится к уравнению в отрезках при : .

Решение типовых задач.

            Пример 1. Точка Р₁(3, -2, 1) является основанием перпендикуляра, опущенного из точки Р₂(5, -5, -3) на плоскость. Составить уравнение плоскости.

            Решение. Пусть текущая (переменная) точка Р(x, y, z) принадлежит данной плоскости. Тогда вектор  принадлежит плоскости, а вектор  перпендикулярен плоскости. Условие перпендикулярности дает векторное уравнение плоскости: , или, в координатной форме,  2(х – 3) – 3(у + 2) – 4(z – 1) = 0, или 2х – 3у – 4z – 8 = 0.