Аналитическая геометрия на плоскости и в пространстве, страница 5

2.1.5. Плоскость в пространстве.

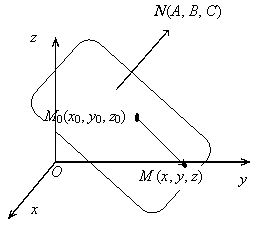            2.1.5.1. Определение плоскости. Векторное уравнение плоскости. Общее уравнение плоскости. Пусть в пространстве задан ненулевой вектор N(A, B, C) и точка М₀(x₀, y₀, z₀). Плоскость задается как геометрическое место точек М (x, y, z) пространства таких, что вектор М₀М ортогонален вектору N. Таким образом, получаем векторное уравнение плоскости

.                                                                                                                                     

(скалярное произведение ортогональных векторов равно нулю). Вектор N называется нормальным вектором плоскости.

            В координатном виде векторное уравнение имеет вид

            А(х – х₀) + В(у – у₀) + С(z – z₀) = 0

(уравнение плоскости, проходящей через точку М₀(x₀, y₀, z₀) и имеющей нормальный вектор N(A, B, C)). Преобразуем это уравнение: Ах + Ву + Сz + (–Ах₀ –Ву₀ –Сz₀) = 0, или Ах + Ву + Сz + D = 0, где D = (–Ах₀ – Ву₀ – Сz₀). 

Уравнение

            Ах + Ву + Сz + D = 0

называется общим уравнением плоскости. Координаты х, у, z  входят в это уравнение в первой степени, поэтому плоскость называют поверхностью первого порядка.

Связкой плоскостей называют совокупность плоскостей, проходящих через одну точку. Очевидно, уравнение А(х – х₀) + В(у – у₀) + С(z – z₀) = 0 при произвольных (не равных нулю одновременно) коэффициентах А, В, С есть уравнение связки плоскостей, проходящих через точку М₀(x₀, y₀, z₀).

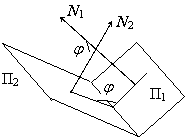2.1.5.2. Угол между плоскостями. Даны две плоскости П₁: А₁х + В₁у + С₁z + D₁ = 0 с нормальным вектором N₁(A₁, B₁, C₁) и П₂: А₂х + В₂у + С₂z + D₂ = 0 с нормальным вектором N₂(A₂, B₂, C₂). Очевидно, косинус угла между плоскостями равен косинусу угла между нормальными векторами, поэтому 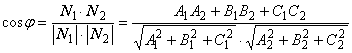. Если требуется определить острый угол между плоскостями, то .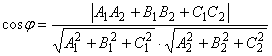

2.1.5.3. Условия параллельности и перпендикулярности плоскостей. Плоскости параллельны тогда и только тогда, когда коллинеарны их нормальные векторы, т.е.условие параллельности прямых имеет вид . Если выполняются равенства , то уравнения А₁х + В₁у + С₁z + D₁ = 0 и А₂х + В₂у + С₂z + D₂ = 0 определяют одну и ту же плоскость.