![]() .
.
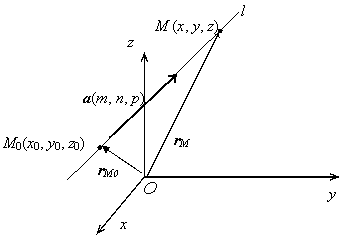
Это уравнение называется векторным уравнением прямой в пространстве. Вектор а называется направляющим вектором прямой.
Запишем векторное уравнение в координатной форме. rМ = xi + yj + zk,
rМ0 = x0 i + y0 j + z0 k, a t = mti + ntj + ptk, поэтому
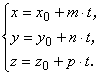
Эти уравнения называется параметрическими
уравнением прямой в пространстве. Исключим из этих уравнений параметр t: ![]() . Уравнения
. Уравнения
![]()
называется каноническими уравнениями прямой в пространстве.
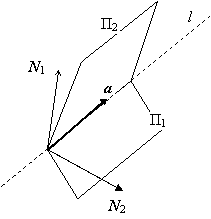 Прямая в пространстве может задаваться также как пересечение
двух непараллельных плоскостей:
Прямая в пространстве может задаваться также как пересечение
двух непараллельных плоскостей:
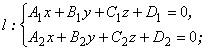 векторы N1(A1, B1,
C1) и N2(A2, B2,
C2) неколлинеарны. Система
векторы N1(A1, B1,
C1) и N2(A2, B2,
C2) неколлинеарны. Система
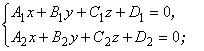 называется общими уравнениями
прямой. Для того, чтобы привести общие уравнения к каноническим или
параметрическим уравнениям, необходимо найти какую-либо точку прямой и ее
направляющий вектор. Для нахождения точки надо решить систему из двух уравнений
с тремя неизвестными; так как векторы N1
и N2 неколлинеарны, один из
миноров матрицы
называется общими уравнениями
прямой. Для того, чтобы привести общие уравнения к каноническим или
параметрическим уравнениям, необходимо найти какую-либо точку прямой и ее
направляющий вектор. Для нахождения точки надо решить систему из двух уравнений
с тремя неизвестными; так как векторы N1
и N2 неколлинеарны, один из
миноров матрицы 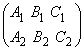 отличен от нуля. Пусть,
например, отличен от нуля минор
отличен от нуля. Пусть,
например, отличен от нуля минор 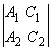 . Задав значение у
произвольно, находим х и z, точка (х,
у, z) и будет точкой прямой. Направляющий
вектор а находится как векторное произведение векторов N1 и N2:
а = N1хN1.
. Задав значение у
произвольно, находим х и z, точка (х,
у, z) и будет точкой прямой. Направляющий
вектор а находится как векторное произведение векторов N1 и N2:
а = N1хN1.
Примеры: 1. Найти канонические и параметрические
уравнения прямой ![]()
Здесь N1
= (2, -3, 4), N2 = (3, 2, -6),
поэтому 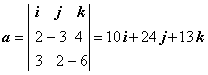 . Для нахождения точки, принадлежащей
прямой, положим , z = 0 (минор
. Для нахождения точки, принадлежащей
прямой, положим , z = 0 (минор ![]() ). Из системы
). Из системы ![]() находим
х = 2, у = 1, следовательно, М0 = (2, 1, 0). Канонические
уравнения прямой:
находим
х = 2, у = 1, следовательно, М0 = (2, 1, 0). Канонические
уравнения прямой: ![]() . Параметрические уравнения
прямой:
. Параметрические уравнения
прямой: 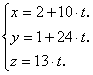
2. Найти канонические и параметрические уравнения прямой, проходящей через две данные точки М1(x1, y1, z1) и М2(x2, y2, z2).
Естественно, в качестве направляющего вектора в
этом случае проще всего взять вектор М1М2(x2 – x1,
у2 – у1, z
2 – z 1), в качестве точки
прямой можно взять любую из точек М1 или М2.
В результате канонические уравнения будут иметь вид ![]() ,
параметрические
,
параметрические 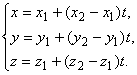
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.