Вычисление жордановой нормальной формы линейного преобразования A:LàLи соответствующего жорданова базиса в случае dim L=3

Г.М. Бродский

Вычисление жордановой нормальной формы линейного преобразования A:LàL и соответствующего жорданова базиса в случае dim L=3
(пособие для студентов)

Ярославль 1998
Вычисление жордановой нормальной формы линейного преобразования A:LàLи соответствующего жорданова базиса в случае dim L=3

Пусть л.п. A:LàL задано своей матрицей [A] в базисе е1, е2, е3 в.п. L. Вычислим его характеристический многочлен FA (l) = |[A] - lE3| и найдём его корни (т.е. собственные значения л.п. A). При этом возможны следующие три случая.

Случай 1.   FA (l) = (l-l1)(l-l2)(l-l3), где l1, l2, l3ÎC[1] – попарно различные числа. Здесь алг. крат. l1=1, алг. крат. l2=1 и алг. крат. l3=1. Но для любого собственного значения l i всегда справедливо неравенство  1 £ геом. крат. l i £ алг. крат. l i. Поэтому в нашем случае геом. крат. l i =dim =1. Следовательно, dim ( Å  Å )= = dim + dim + dim = 3, т.е.  Å  Å  = L. Отсюда вытекает, что л.п. A диагонализируемо и его ж.н.ф. такова:

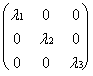
Случай 2. FA (l) = – , где l1, l2 Î C и l1¹l2.  Здесь алг. крат. l1 = 2
и алг. крат. l2 = 1. Так же, как и в случае 1, выводим, что геом. крат. l2 = 1. Поскольку 1 £ геом. крат. l1  £ алг. крат. l1=2, разобьём случай 2 на два.

Случай 2а.  Геом. крат. l1 = dim  = 2. Тогда dim ( Å ) = 3,
т.е.  Å  = L. Отсюда вытекает, что л.п. A диагонализируемо и его ж.н.ф. такова:

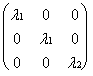
Случай 2б. Геом. крат. l1  = 1. Тогда из теоремы о связи геометрической кратности с ж.н.ф. следует, что в ж.н.ф. л.п. A будет одна жорданова клетка с l1 на главной диагонали (второго порядка, т.к. алг. крат. l1 = dim = 2) и одна жорданова клетка с l2 на главной диагонали. (первого порядка, т.к. алг. крат. l2 = dim = 1). Итак, ж.н.ф. имеет вид:

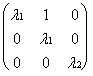
Случай 3. , где l1  Î С. Здесь алг. крат. l1  = 3. Поскольку 1 £ геом. крат. l1  £ алг. крат. l1=3, разобьём случай 3 на три.

Случай 3а. Геом. крат. l1 = dim = 3. Тогда = L, так что A диагонализируемо и его ж.н.ф.

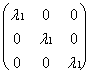
Случай 3б. Геом. крат. l1 = 2. Тогда по теореме о связи геометрической кратности с ж.н.ф. в ж.н.ф. л.п. A будет две жордановых клетки с l1 на главной диагонали. Поскольку они должны заполнить матрицу третьего порядка, одна из них будет порядка 2, а другая – порядка 1. Таким образом, ж.н.ф. имеет вид: