Вычисление жордановой нормальной формы линейного преобразования A:LàLи соответствующего жорданова базиса в случае dim L=3, страница 4

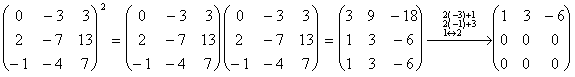
Общее решение  . Строим начальный базис подпространства L2, дополняя базис (3, 1, 1) подпространства L1  векторами из базиса (3, -1, 0), (6, 0, 1). Это можно сделать, например, так: (3, 1, 1),
(3, -1, 0) (эта система векторов, очевидно, линейно независима).

Теперь найдём базис подпространства L3. Можно это сделать, вычисляя

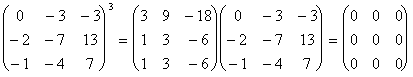
Однако можно обойтись и без этого, используя соображение, аналогичное замечанию 3. А именно, из соотношений L2 Î  = L и dim L2 = 2 вытекает, что L2 Ï L3 и
2 = dim L2 < dim L3 £ 3. Поэтому dim L3 = 3, т.е. L3 = L и в качестве базиса подпространства L3 можно взять (1, 0, 0), (0, 1, 0), (0, 0, 1). Строим начальный базис подпространства L3, дополняя начальный базис (3, 1, 1), (3, -1, 0) подпространства L2 векторами из базиса (1, 0, 0), (0, 1, 0), (0, 0, 1). Это можно сделать, например, так: (3, 1, 1), (3, -1, 0),
(0, 0, 1) (легко выяснить, что эта система векторов линейно независима). Корневые векторы (3, 1, 1), (3, -1, 0) и (0, 0, 1) имеют высоты 1, 2 и 3 соответственно (первый из L1, второй из L2\L1, третий из L3\ L2). Остаётся из корневого вектора (0, 0, 1) высоты 3 вытащить серию и взять соответствующую обратную серию. Сделаем это. Имеем:
u1  = (0, 0, 1),   ,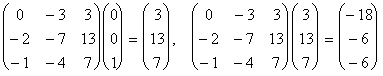
т.е. u2 = (3, 13, 7), u3 = (-18, -6, -6).

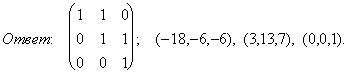
Проверка:

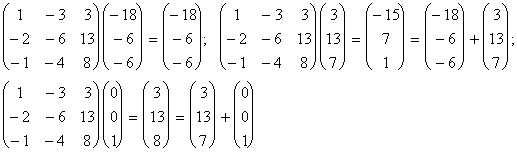
Замечание 4. В случае 3в вычисление жорданова базиса сводится к нахождению корневого вектора высоты 3. Поэтому можно было не находя начального базиса подпространства L2 использовать вместо него базис (3, -1, 0), (6, 0, 1). Более того, можно было вообще не находить базис подпространства L2 , заметив, что в случае 3в хотя бы один из векторов (1, 0, 0), (0, 1, 0), (0, 0, 1) является корневым вектором высоты 3. Такой вектор легко обнаружить вытаскиванием серий из векторов (1, 0, 0), (0, 1, 0), (0, 0, 1).