Вычисление жордановой нормальной формы линейного преобразования A:LàLи соответствующего жорданова базиса в случае dim L=3, страница 3

Ответ: 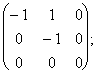     (6, 6, -8), (3, 1, 0), (2, 1, -1).

Проверка:

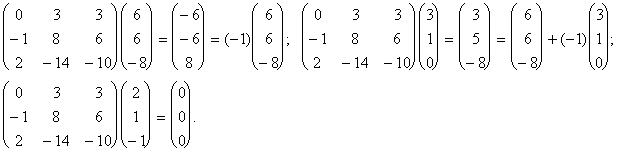
Пример 3а. Пусть [A] =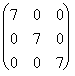

Ответ: ;      (1,0,0), (0,1,0), (0,0,1).

Замечание 2. Более сложных задач в случае 3а не существует. Действительно, жорданова нормальная форма в случае 3а является скалярной матрицей:

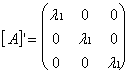
Поэтому [A]’ коммутирует с любой матрицей из Mat 3 (). Обозначив через C матрицу перехода от базиса е1, е2, е3 к жорданову базису, имеем:

Пример 3б. Пусть [A] =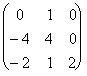

1)  Тогда FA (l) = , т.е. l1  = 2. Для единственного собственного значения l1=2 ищем начальные базисы подпространств Li (i = 1, 2,...).

Сначала найдём базис подпространства L1  = .

Начальный базис подпространства L1  найден: (1, 2, 0), (0, 0, 1), (1, 0, 0). Видим, что геом. крат. l1  = 2 и мы имеем случай 3б.

Теперь найдём базис подпространства L2.

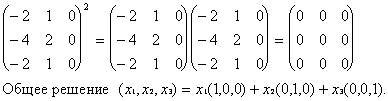
Строим начальный базис подпространства L2, дополняя базис (1,2,0), (0,0,1) подпространства L1  векторами из базиса (1,0,0), (0,1,0), (0,0,1). Это можно сделать, например, так: (1,2,0), (0,0,1), (1,0,0) (легко видеть, что эта система векторов линейно независима). Поскольку L2 = L, то L3 не надо рассматривать.

Высоты векторов из построенного начального базиса подпространства L2 таковы: (1,2,0) и (0,0,1) высоты 1 (они принадлежат L1); (1,0,0) высоты 2 (он принадлежит L2\ L1). Из корневого вектора (1,0,0) высоты 2 вытаскиваем серию: u1  = (1,0,0);

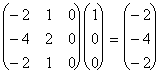, т.е. u2 = (-2,-4,-2). Вектор u2 является корневым вектором высоты 1 (т.е. собственным вектором). Дополняем вектор u2 = (-2,-4,-2) до базиса подпространства L1 векторами из базиса (1,2,0), (0,0,1). Это можно сделать, например, так:
(-2,-4,-2), (0,0,1) (легко видеть, что эта система векторов линейно независима). Вектор (0,0,1) собственный и потому совпадает со своей обратной серией. Выписывая найденные обратные серии, получаем жорданов базис.

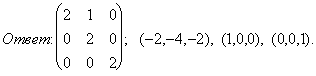
Проверка:

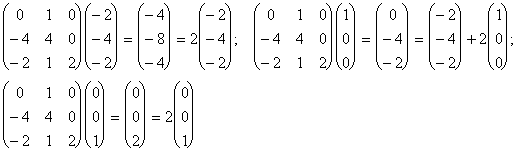
Замечание 3. В примере 3б выкладки можно было бы немного сократить, если бы после вычисления геом. крат. l1 мы заметили, что из соотношений что L1 Ë L2 и 2 = dim L1 < dim L2 £ 3. Поэтому dim L2 = 3, т.е. L2 = L и в качестве базиса подпространства L2 можно взять (1,0,0), (0,1,0), (0,0,1). Это позволяет избежать возведения матрицы 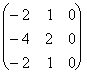в квадрат.

Пример 3в.  Пусть [A] =

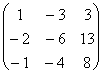
1)  Тогда FA (l) = , т.е. l1  = 1. Для единственного собственного значения l1=1 строим начальные базисы подпространств Li (i = 1, 2,...).

Сначала найдём базис подпространства L1  = .

Начальный базис подпространства L1  состоит из одного вектора (3, 1, 1). Видим, что геом. крат. l1  = 1, т.е. мы имеем случай 3в.

Теперь найдём базис подпространства L2.