Определение функции непрерывной в точке и векторной функции скалярного аргумента

                                     Билет № 30.

Дать определение функции непрерывной в точке (привести равносильные формулировки) и доказать теорему о переходе к пределу под знаком непрерывной функции (limf[g(x)] = f [limg(x)]).

^{x – a                                x – a}

Пусть функции f(x) определена в некоторой окрестности точки x₀ (и в самой точки x₀). Функция f(x) называется непрерывной в точке x₀  ó существует lim f(x) = f(x₀)

                         ^{x – x0}

Определение по Коши: Функция f(x) называется непрерывной в точке x₀  ó

 

Определение по Гейне: Функция f(x) называется непрерывной в точке x₀  ó

Теорема о переходе к пределу под знаком непрерывной функции:

Пусть существует lim f(x) = a, и функция Y(y) непрерывна в точке a. Тогда если в некоторой проколотой окрестности * определена сложная функция Y(f(x)), то  limY(f(x)) = Ylimf(x) = Y(a)

^{x -- *                                   x -- *}

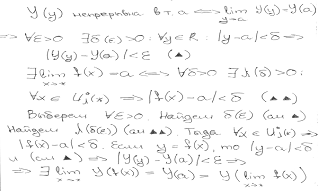(знак предела и непрерывной функции можно переставлять местами). Доказательство:

, ч.т.д.

Дать определение векторной функции скалярного аргумента:  и её производной. Касательная к пространственной кривой. Доказать теорему о производной векторной функции постоянной длины.

Рассмотрим [a,b]. Пусть любому поставлен в     соответствии некоторый вектор , тогда говорят, что на [a,b] задана векторная функция скалярного аргумента.

Пусть задана ортонормированная система координат с базисом , тогда

Функции x(t), y(t), z(t)- скалярные функции действительного аргумента – координатные функции для вектор-функции .

Геометрический смысл векторной функции:

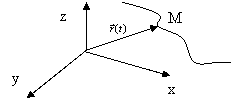Функции

соответствует некоторая кривая

Такое представление кривой называют годографом.  называется пределом функции скалярного аргумента при  если:

.

Рассмотрим приращение векторной функции, придадим t приращение , тогда

.

Производной в точке  называется предел разностного отношения при