Определение функции непрерывной в точке и векторной функции скалярного аргумента, страница 2

, .

, .

Пусть . Предельное положение секущей  при  называют касательной к кривой Г в точке .  . Тогда при  касательная в точке  параллельна вектору . Уравнение касательной: .

- каноническое уравнение касательной.

Теорема: Пусть векторная функция скалярного аргумента ,  - является непрерывно-дифференцируемой функцией на , которой соответствует некоторая кривая Г: . Тогда длина дуги Г удовлетворяет:  (при этом Г имеет конечную длину).

Доказательство: , где , по условию теоремы, функция непрерывно-дифференцируема, значит  на отрезке  - непрерывная функция. ,  (по 1 теореме Вейерштрасса). при.

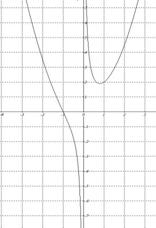
       f (x) = (x^3 + 1)/x

      1. ОДЗ: x – R\{0}

       2. функция общего вида, не периодичная.

        3. асимптоты:

          вертикальных асимптот нет

          горизонтальных асимптот нет

          4. 1 производная

        f’(x)=(3*x^2*x-(x^3+1))/x^2

         экстремумы: min: x = 0.79, y = 1.89.

        5. 2 производная

         f’’(x)=((3*2*x*x+3*x^2-3*x^2)*x^2-(3*x^2*x-(x^3+1))*2*x)/(x^2)^2

         точки перегиба: x = 0, y = ∞

                                       x = -1, y = 0

          6. Нули f(x): x = -1 (y = 0)