Параллельное программирование: Учебное пособие, страница 34

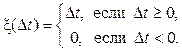
Введенной функцией можно условно (с точностью до постоянного множителя) характеризовать объем вычислительной работы, приходящийся на отрезок перекрытия. Например,

 и                                                                  (2.36)

определяют объемы работ соответственно для случаев, когда длительность процесса  накрывает только левую границу  или только правую .

Есть еще два случая перекрытия межграничного интервала и интервала , которые характеризуются следующими объемами работ:

·  если ранний срок начала выполнения процесса () и поздний срок окончания выполнения процесса  заключены внутри интервала , то есть ;

·  если интервал  лежит внутри интервала i-того процесса, ограниченного слева поздним сроком начала его выполнения оператора  и справа – ранним сроком его окончания , что равносильно выполнению условия  .

Таким образом, для оценки минимальной функции загрузки любого интервала  необходимо для каждого процесса вычислять объемы работ по всем перечисленным случаям, брать из них наименьшее значение и находить сумму объемов работ по всем процессам:

Если интервал  изменять перебором всех допустимых значений , придавая им значения дискретных моментов времени , то оценивая по (2.35) потребное число процессоров, можно найти их минимальное число, которое необходимо при заданной длительности выполнения параллельного алгоритма. Если же фиксировать число процессоров на уровне меньшем, чем их минимально возможное число, то за счет одновременного отодвигания поздних сроков окончания выполнения всех вершинных процессов, можно будет поставить вопрос о нахождении минимального времени выполнения всего параллельного алгоритма.

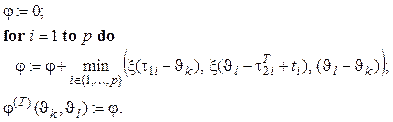                    (2.37)

Ядром алгоритмов вычисления максимального числа процессоров при их минимальной загрузке на всех интервалах и поиска минимального времени выполнения параллельного алгоритма для заданного их числа служат выражения (2.34, 2.35), которые включают алгоритм вычисления функции минимальной загрузки интервала (2.37). Вложенные друг в друга циклы обеспечивают для ядра перебор допустимых значений границ интервала .

proc nmax( )

;  ;

begin

;

;

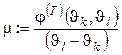end;

end;

end.

Вариант псевдокода, минимизирующего время выполнения алгоритма на  процессорах, представлен ниже.

proc tmin( );

;

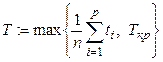;     // здесь  единица измерения временных параметров

;

begin

;

 begin;

 end;   // () – временное смещение поздних сроков

end;

end.

2.4  Организация взаимного обмена данными.

Рассмотренные формальные методы распараллеливания процессов и оптимального их размещения по процессорам и во времени позволяют весь вычислительный процесс сконфигурировать так, что готовность всех данных, определяющих запуск любого процесса, всегда произойдет. Однако некоторые особенности взаимного расположения взаимодействующих процессов и их влияние на время выполнения всего алгоритма, например, можно обсудить, если на рисунок 2.16в нанести все информационные связи. Эти связи на рисунке 2.17 показаны в условно расширенных промежутках между отдельными процессами с сохранением одновременности начал процессов, находящихся на разных машинах.

Во-первых, необходимо отметить не единственность существования нескольких оптимальных во времени размещений процессов и их начал. Во-вторых, выделяются своей неподвижностью по отношению друг к другу процессы, образующие путь с критическим временем. И, в-третьих, не однозначность закрепления отдельных процессов или групп процессов за конкретными процессорами.

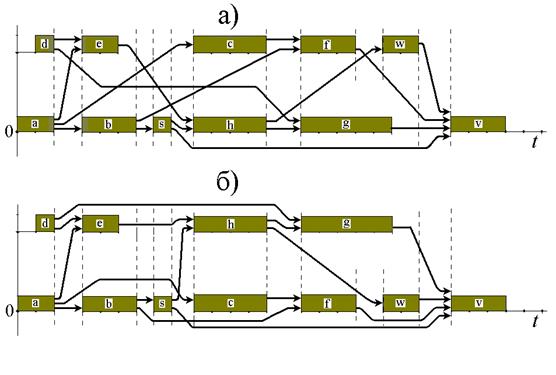Рисунок 2.17.