Этот простой пример показывает, насколько разнообразными могут быть параллельные формы алгоритмов, построенные для одной и той же задачи. Отметим некоторые поучительные моменты, связанные с заданием порядка выполнения действий, полученных путем применения законов ассоциативности, дистрибутивности и коммутативности.
Среди приведенных форм отметим форму (d), которая содержит наименьшее число операций: шесть. В выражении этой формы все переменные встречаются только один раз! Глубина алгоритма (число ярусов) равна числу операций. На каждом ярусе степень параллелизма равна единице (ширина алгоритма), поэтому все операции последовательно могут быть выполнены на одном процессоре. Эта форма алгоритма реализует схему вычисления по Горнеру, которая среди последовательных алгоритмов, вычисляющих значения степенных полиномов, считается наилучшей по быстродействию.
Форма (a) построена по исходному выражению, в котором без изменения порядка переменных расставлены скобки, то есть, применен ассоциативный закон, выделивший пары операндов для очередной операции. Благодаря этому уменьшено число ярусов до четырех, но расплачиваться за это пришлось увеличением ширины алгоритма до трех на первом и втором ярусах. Выгода в быстродействии получена. Правда, для реализации этой параллельной формы потребуется применить три процессора. Ускорение вычислений с тремя процессорами при одинаковых длительностях операций сложения и умножения будет равно
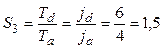 .
.
Полученное ускорение было вычислено путем сопоставления времени вычислений по параллельному алгоритму со временем максимально быстрого вычисления последовательного алгоритма для одного процессора. Однако количество операций в сопоставляемых алгоритмах различное за счет того, что ряд операндов в параллельном алгоритме формы (а) повторяется в некоторых двуместных операциях несколько раз. В том случае, когда каждая из операций будет составной и, следовательно, вычислительный процесс с операндами ею порожденный, будет иметь свою, неповторимую длительность, придется при расчете ускорения учитывать общее число операций в параллельном алгоритме.
В аналитической литературе по распараллеливанию алгоритмов постулируется, что каждый операнд из n операндов должен входить в вычисляемое выражение ровно один раз. Это условие не приводит к потере общности, потому что с помощью переименования переменных всегда можно добиться его выполнения [1].
В силу указанных причин, ускорение в каждом конкретном случае должно вычисляться с использованием в числителе времени, которое потребовалось бы одному процессору на вычисление всех операций. С учетом сказанного, для алгоритма (а) время в числителе формулы расчета ускорения должно составить 9 единиц (по числу операций), а время в знаменателе – по числу уровней, то есть 4:
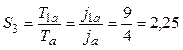 ,
,
где ![]() – время, которое
затратил бы один процессор на все операции.
– время, которое
затратил бы один процессор на все операции.
Средняя степень параллелизма для
формы (а) при условии, что каждый уровень затрачивает на вычисление одной
операции одну единицу времени, то есть ![]() , может
быть вычислена по формуле (1.1):
, может
быть вычислена по формуле (1.1):
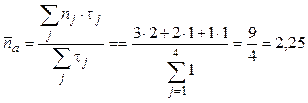 .
.
Полученная средняя степень параллелизма, близкая к двум, порождает желание продолжать преобразование исходного выражения, используя кроме ассоциативного закона еще и законы дистрибутивности и коммутативности. Объединив первое и четвертое слагаемое в одну группу, а из второго и третьего вынеся за скобки общую переменную, можно получить параллельную форму (b) всего лишь с восемью операциями. И хотя средняя степень параллелизма теперь окажется равной двум, и ускорение будет равно двум, однако для реализации его на параллельной системе все равно потребуется три процессора:
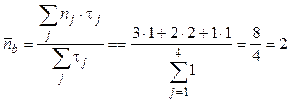 ;
; 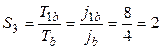 .
.
Примечательно то, что, поразмыслив над исходным выражением и перегруппировав слагаемые, можно уменьшить число операций еще на одну. Параллельная форма алгоритма (с) может быть выполнена за те же четыре единицы времени, но уже на двух процессорах. Средняя степень параллелизма и ускорение будут соответственно равны:
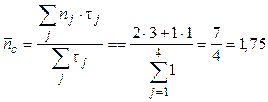 ;
; 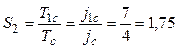 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.