Параллельное программирование: Учебное пособие, страница 18

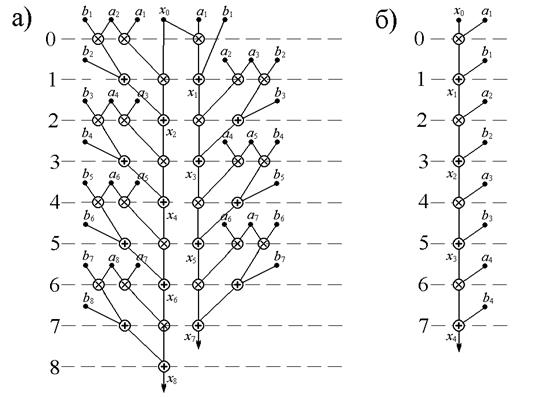
Вычисление выражений в скобках можно проводить одновременно с вычислением рекуррентных соотношений. Каждая из рекурсий с применением неограниченного параллелизма вычисляет очередное значение с шагом в две единицы. Вычисление же  двух последовательных значений линейной рекурсии первого порядка в однопроцессорном варианте требует четырех уровней, то есть вдвое больше. На рисунке 2.5 изображены эти две формы пошаговых алгоритмов.

Сравнивая две формы алгоритмов вычисления одной и той же рекурсии, мы наглядно видим ту цену, которую необходимо заплатить за ускорение вычислений всего лишь в два раза: число процессоров возросло в 5 раз! При этом естественно возникнут дополнительные расходы времени на обмен данными и сборку результатов. Однако кое-что полезное от исходной рекурсии сохранилось. В распараллеленной форме этим полезным является регулярность структуры. Пары уровней {2, 3}, {4, 5}, ..., {2i, 2i+1} имеют тождественные параллельные формы и отличаются только входными и выходными параметрами.

Если в конструкциях операторов языка программирования будет позволено подставлять в качестве фактических параметров процедур или функций имена процессоров, то весь алгоритм в принципе будет представим в виде цикла, телом которого окажется эта процедура или функция. В свою очередь, каждый из двух уровней тела цикла из-за различия в векторе входных/выходных данных каждого уровня тоже может быть оформлен в виде процедуры или функции.

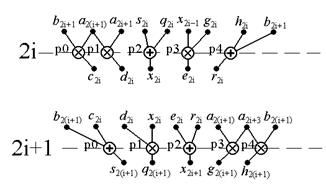Рисунок 2.6.

На рисунке 2.6 две повторяющиеся одноуровневые параллельные структуры выделены в отдельные образования, на которых отображены операнды, представляющие собой возможные формальные параметры некоторых обобщенных процедур. С точки зрения программирования и создания текстов программ, указанные образования в большинстве случаев могут оказаться не очень разумными, так как вовлекают в процесс компиляции процессы, располагаемые на разных процессорах, связанных в общем случае коммуникационной средой с заранее неизвестной конфигурацией. В настоящее время ни один из распространенных языков программирования высокого уровня в полной мере такими компилирующими свойствами еще не обладает. Лучшее, что здесь видится и часто реализуется (об этом речь пойдет ниже), так это выделение из параллельных форм заданного числа параллельно исполняемых ветвей, каждая из которых включает отдельные фрагменты задачи, которые располагают в пределах одного вычислительного модуля (процессора). Процессы, описываемые фрагментами, представляются и последовательно выполняться как последовательный единый процесс с временными задержками и остановками лишь для реализации функций взаимодействия с процессами ветвей, размещенных на других процессорах. На рисунке 2.7 показано возможное распределение вычислительных фрагментов по процессорам с указанием тех промежуточных значений, которые обязаны пересылаться из одной группы процессоров в другие в одно и то же время.

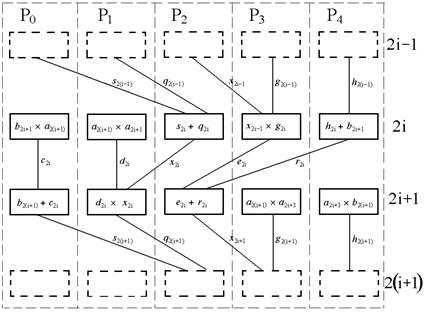Рисунок 2.7.

Переход с уровня на уровень требует три межпроцессорные пересылки промежуточных данных. Исходные массивы операндов заранее должны быть загружены в память процессоров Р₀, Р₁, Р₃, Р₄. Массив результатов рекурсивных вычислений будет формироваться в процессоре Р₂.

2.2.4  Преобразование общих рекуррентных выражений

Общей рекуррентной задачей  порядка m называют задачу вида

,                                    (2.5)

где      – рекуррентная функция в общем случае нелинейная;

 –  заданных начальных значений;

 – векторы параметров, независящие от .

Рассмотренные выше рекурсивные функции были линейными и благодаря этому обладали в определенной мере ассоциативными свойствами.

Наиболее простые рекурсии, в которых отсутствовало чередование различных операций, приводили нас к многоярусным параллельным формам с ассоциативным сдваиванием исходных и промежуточных операндов. Глубина этих форм выражалась двоичным логарифмом числа исходных данных. Поэтому важно находить такие преобразования рекурсий, которые могли бы в конечном (преобразованном) виде подчиняться ассоциативному закону в форме сдваивания.