Параллельное программирование: Учебное пособие, страница 16

Более быстрые параллельные формы, полученные из выражений (a, b, c) и эквивалентные схеме Горнера (d), содержат больше операций, чем в последовательной форме (d). Более того, доказана теорема, что для произвольного алгоритма вычисления обобщенной схемы Горнера

имеет место следующее соотношение, которое связывает время вычисления t, равное числу уровней j при одинаковых длительностях операций, число операндов  и число операций :

.

Для рассмотренного примера  и , т. е. . Подстановка подтверждает значение  для  формы алгоритма (d):

                                .

2.2.2  Алгоритмы сдваивания

Альтернированное выражение (2.1) после раскрытия в нем всех скобочных форм и сохраняющее свойство ассоциативности позволяет построить некоторую параллельную форму, что мы и видели в предыдущем разделе. Если в развернутом выражении все двуместные операции будут одного и того же вида, то, взяв в скобки пары рядом стоящих операндов, мы получим первый ярус вычислений с максимальным количеством операций, которые можно выполнять одновременно.

Над результатами операций первого яруса можно произвести аналогичные ассоциативные расстановки скобок. Операцию ассоциативного преобразования результатов каждого яруса можно продолжать до тех пор, пока на последнем ярусе останется лишь одна пара операндов. Такой алгоритм получения параллельной формы называется алгоритмом сдваивания. На рисунке 2.3  приведена параллельная форма алгоритма сдваивания. В нем выполняется суммирование n чисел.

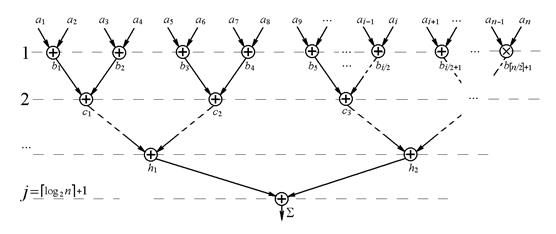Рисунок 2.3.

Если , то число уровней суммирования окажется равным j. Если  и  n – нечетное, то на первом уровне для суммирования потребуется  процессоров, где  – наименьшее целое, не меньше . Столько же будет промежуточных значений частичных сумм . На втором уровне потребуется  процессоров, если  – тоже нечетное, иначе . Продолжая такое суммирование до конечного результата, мы в целом пройдем число уровней, равное

.                                 (2.2)

В методе сдваивания при построении параллельной формы алгоритма максимальная степень параллелизма приходится на первый уровень и составляет , если . С каждым переходом на один уровень ниже, параллелизм уменьшается в два раза. На последнем уровне степень параллелизма равна единице, следовательно, среднюю степень параллелизма можно выразить суммой общего числа операций, разделенной на число j уровней, следующим образом:

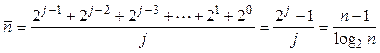.            (2.3)

Целью построения параллельных форм алгоритмов, кроме достижения минимальной глубины, немаловажную роль играет и достижение высокой эффективности использования вычислительного оборудования. Речь идет о максимальной загрузке параллельно работающих процессоров или минимизации времени вынужденного простоя, когда тот или иной процессор закончил свой процесс и данных для продолжения его работы уже нет.

Сто процентная загрузка оборудования соответствует случаю, когда все параллельные процессоры ни на миг не приостанавливают своей работы от начала параллельного алгоритма до его завершения. Это равносильно варианту, когда при p процессорах на каждом уровне алгоритма задействованы все p процессоров. Алгоритм сдваивания очевидным образом к такому варианту не относится, так как число процессоров, выбранное по  максимальной степени параллелизма, на нижних уровнях систематически уменьшается. В этом случае повысить эффективность использования оборудования можно лишь искусственным уменьшением ширины параллельной формы до числа процессоров не менее , то есть до среднего числа, округленного до ближайшего целого.

В общем случае эффективность использования оборудования при решении конкретной параллельной задачи на p процессорах представляют отношением

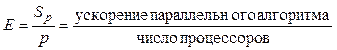.            (2.4)

Поскольку обычно , то .

Для алгоритма сдваивания глубина параллельной формы оценивается в общем случае выражением (2.2), а максимальное число операций последовательного эквивалентного алгоритма суммирования несложно подсчитать: оно равно . Ускорение параллельного алгоритма сдваивания можно представить следующим выражением: