![]() .
.
Если взять ![]() процессоров, то эффективность их
использования можно оценить так:
процессоров, то эффективность их
использования можно оценить так:
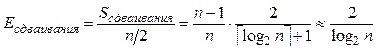 .
.
Для ![]() эффективность
будет меньше
эффективность
будет меньше ![]() и с увеличением n
будет уменьшаться и далее.
и с увеличением n
будет уменьшаться и далее.
Выходом может служить ограничение числа процессоров по сравнению с максимальным числом, равным максимальной степени параллелизма, например, выбрав это целое число близким к средней степени параллелизма.
В отличие от (2.3), при произвольном n, средняя степень параллелизма алгоритма сдваивания должна быть записана со знаменателем из (2.3) и, следовательно, взяв число процессоров, равное
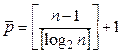 ,
,
можем без увеличения числа уровней параллельного алгоритма достигнуть эффективности порядка
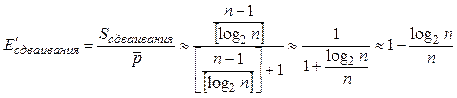 ,
,
где ![]() – значение выражения в
квадратных скобках, округленное до ближайшего целого.
– значение выражения в
квадратных скобках, округленное до ближайшего целого.
Построение параллельного алгоритма со степенью параллелизма меньшей, чем максимальная степень и средняя степень, позволяет при незначительном увеличении глубины достигнуть существенно большей эффективности использования оборудования.
Для примера рассмотрим
суммирование ![]() операндов на
операндов на ![]() процессорах
методом сдваивания. Максимальная степень параллелизма для этого количества
операндов составляет
процессорах
методом сдваивания. Максимальная степень параллелизма для этого количества
операндов составляет ![]() , число уровней суммирования
, число уровней суммирования ![]() . Ускорение по сравнению с последовательным
алгоритмом в
. Ускорение по сравнению с последовательным
алгоритмом в ![]() раза. При девяти процессорах
эффективность использования оборудования составит
раза. При девяти процессорах
эффективность использования оборудования составит ![]() .
.
На рисунке 2.4а приведена схема параллельной структуры с пятью уровнями суммирования и максимальной степенью параллелизма, равной 9, а на рисунке 2.4б – параллельная структура суммирования с использованием лишь пяти процессоров.
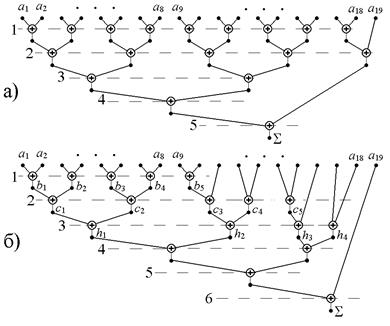 |
Рисунок 2.4.
Число уровней суммирования с
параллелизмом ![]() составит
составит ![]() .
Остаток неохваченных суммированием данных
.
Остаток неохваченных суммированием данных ![]() . На
последующих уровнях к промежуточным значениям, полученных суммированием на
уровнях
. На
последующих уровнях к промежуточным значениям, полученных суммированием на
уровнях ![]() , необходимо добавлять значения исходных
операндов, неохваченных еще суммированием, и к ним применять процедуру
сдваивания. Для рассматриваемого примера новое количество данных составит
, необходимо добавлять значения исходных
операндов, неохваченных еще суммированием, и к ним применять процедуру
сдваивания. Для рассматриваемого примера новое количество данных составит ![]() . На них можно сформировать еще уровни с
параллелизмом
. На них можно сформировать еще уровни с
параллелизмом ![]() :
: ![]() ;
; ![]() . Очередной набор промежуточных данных для
сдваивания составит
. Очередной набор промежуточных данных для
сдваивания составит ![]() . Полученное количество
промежуточных данных для сдваивания меньше
. Полученное количество
промежуточных данных для сдваивания меньше ![]() ,
поэтому последующие уровни суммирования будут иметь уменьшающуюся степень
параллелизма.
,
поэтому последующие уровни суммирования будут иметь уменьшающуюся степень
параллелизма.
Для параллельной формы общее
число уровней суммирования ![]() , ускорение
, ускорение ![]() и эффективность
и эффективность ![]() .
.
Рекуррентные выражения (рекурсии) встречаются при решении многих задач вычислительной математики. Рекуррентным выражением порядка k является формула вычисления значения операнда следующего вида:
![]() .
.
При ![]() каждый член
последовательности
каждый член
последовательности ![]() выражается через предыдущие k членов
выражается через предыдущие k членов ![]() . Для начала рекуррентного вычислительного
процесса необходимо знать k первых членов
последовательности
. Для начала рекуррентного вычислительного
процесса необходимо знать k первых членов
последовательности ![]() , то есть – (
, то есть – (![]() ).
).
Частными случаями рекуррентных выражений являются формулы вычисления членов арифметической и геометрической прогрессии, схема Горнера, рассмотренная ранее, выражения для вычисления значений ортогональных многочленов, например, полиномов Чебышева первого рода
![]() ,
,
суммирование значений
числовых или функциональных рядов, вычисление подходящих целых дробей для
заданной, например, бесконечной цепной дроби 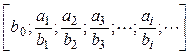 в
виде
в
виде
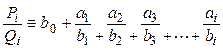 ,
,
в
которых при 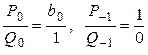 ,
,
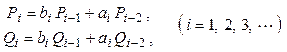 ,
,
а также вычисление или преобразование аналогичных рекуррентных формул с операндами и коэффициентами векторного и/или матричного типов.
Рекурсии в общем случае могут быть нелинейными.
Наиболее часто в вычислениях встречаются линейные рекурсии первого порядка:
![]() .
.
Это сугубо последовательный процесс, так как
каждое ![]() не может быть вычислено, пока неизвестно
значение
не может быть вычислено, пока неизвестно
значение ![]() . Для вычисления
. Для вычисления ![]() потребуется
2n операций или тактов, если операции одинаковы
по длительности. Однако если объединить в одно выражение две соседние по
индексу строки исходной рекурсии, то можно получить две рекурсивные
последовательности, сдвинутые по индексу относительно друг друга на единицу:
потребуется
2n операций или тактов, если операции одинаковы
по длительности. Однако если объединить в одно выражение две соседние по
индексу строки исходной рекурсии, то можно получить две рекурсивные
последовательности, сдвинутые по индексу относительно друг друга на единицу:
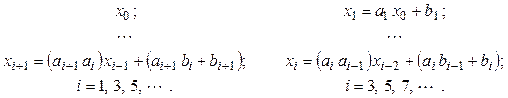
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.