где ![]() – блочные матрицы
параметров
– блочные матрицы
параметров ![]() и
и
![]() –
блочные векторы размерности 4,
–
блочные векторы размерности 4,
представляется матрицами и векторами больших размеров:
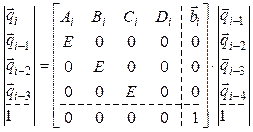 .
.
Обозначив полученную матрицу размера ![]() через
через ![]() и
результирующий вектор размера
и
результирующий вектор размера ![]() через
через ![]() , матричную рекурсию четвертого порядка
запишем в следующем виде:
, матричную рекурсию четвертого порядка
запишем в следующем виде:
![]() ,
,
где ![]() – заданный начальный вектор.
– заданный начальный вектор.
Матричное произведение в скобках можно вычислить
методом сдваивания с макро операцией умножения двух матриц размера ![]() за
за ![]() макро
шагов, используя при этом
макро
шагов, используя при этом ![]() процессоров.
Многократное применение процедуры сдваивания при переходе с уровня на уровень
при вычислении рекурсий получило название процесса рекуррентного сдваивания.
процессоров.
Многократное применение процедуры сдваивания при переходе с уровня на уровень
при вычислении рекурсий получило название процесса рекуррентного сдваивания.
Важной особенностью, рассмотренного подхода к распараллеливанию, является возможность за один шаг вычислять целый блок промежуточных значений рекуррентной последовательности. Однако есть рекуррентные функции, которые требуют специальных подходов к выделению или построению выражений для блоков с параллельно вычисляемыми значениями рекуррентной последовательности. К этой категории задач можно отнести обыкновенные дифференциальные уравнения с начальными условиями.
Пусть задано следующее дифференциальное уравнение первого порядка в обыкновенных производных
![]() . (2.9)
. (2.9)
Вычисление значений искомой функции ![]() возможно лишь в том случае, если
производную
возможно лишь в том случае, если
производную ![]() заменить аппроксимирующим выражением,
использующим только арифметику машинных операции со скалярными операндами.
Такая замена осуществляется на основе аппарата конечных разностей [17], в
рамках которого оператор дифференцирования
заменить аппроксимирующим выражением,
использующим только арифметику машинных операции со скалярными операндами.
Такая замена осуществляется на основе аппарата конечных разностей [17], в
рамках которого оператор дифференцирования ![]() связывается
с операторами повторных конечных разностей “вперед” и, в конечном счете, с
ординатами искомой функции
связывается
с операторами повторных конечных разностей “вперед” и, в конечном счете, с
ординатами искомой функции ![]() , следующим образом:
, следующим образом:
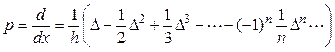 , (2.10)
, (2.10)
где ![]() – оператор конечной разности такой, что
– оператор конечной разности такой, что ![]() ;
;
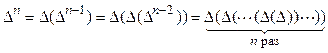 – повторная разность;
– повторная разность;
![]() – шаг по оси
действительной переменной x.
– шаг по оси
действительной переменной x.
Замена в уравнении (2.9) производной ![]() самым простым конечно-разностным
аппроксимирующим выражением приводит к известной формуле Эйлера интегрирования
дифференциальных уравнений от точки к точке:
самым простым конечно-разностным
аппроксимирующим выражением приводит к известной формуле Эйлера интегрирования
дифференциальных уравнений от точки к точке:
![]() . (2.11)
. (2.11)
Для итерационного уточнения полученного значения ![]() формулу (2.11) модифицируют, подставляя в
нее среднее значение от производных в точке
формулу (2.11) модифицируют, подставляя в
нее среднее значение от производных в точке ![]() и
и ![]() :
:
![]() (2.12)
(2.12)
Последовательное приближение проводят несколько раз,
контролируя либо число итераций ![]() , либо достижение
заданной погрешности, после чего переходят к вычислению искомой функции в
следующей точке.
, либо достижение
заданной погрешности, после чего переходят к вычислению искомой функции в
следующей точке.
![]() . (2.13)
. (2.13)
Описанный рекуррентно-итерационный процесс распараллелить невозможно. Однако можно поступить так:
·
по формуле Эйлера (2.11) с шагом ![]() вычислить
значения функции
вычислить
значения функции ![]() в точках
в точках ![]() ;
;
·
на известных в точках ![]() значениях производных
значениях производных ![]() строится интерполяционный многочлен
Ньютона для равных промежутков
строится интерполяционный многочлен
Ньютона для равных промежутков ![]() в виде взвешенной суммы
ординат производных;
в виде взвешенной суммы
ординат производных;
·
приращения функции получают, интегрируя этот многочлен на
интервалах ![]() , и добавляют к значению
, и добавляют к значению ![]() , в результате чего образуется блок
рекуррентных выражений для параллельного вычисления
, в результате чего образуется блок
рекуррентных выражений для параллельного вычисления ![]()
·
выполнением (r) итераций уточняют
полученные значения функции ![]() .
.
Двухточечный блок, сформированный по описанному правилу для уравнения (2.9), в параллельном варианте представляется следующими группами выражений, размещенных на разных процессорах:
Р0 Р1 (2.14)
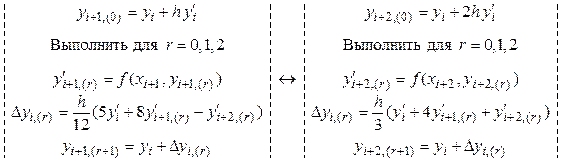
Три итерации при вычислении значений ![]() обеспечивают погрешность, пропорциональную
четвертой степени шага h. В пределах каждого
итерационного цикла необходимо обмениваться значениями
обеспечивают погрешность, пропорциональную
четвертой степени шага h. В пределах каждого
итерационного цикла необходимо обмениваться значениями ![]() ,
,
![]() – для последующего вычисления приращений
функции
– для последующего вычисления приращений
функции ![]() .
.
Аналогичным образом можно сформировать блок формул для одновременного вычисления четырех значений переходного процесса, имеющего шестой порядок точности. Значение каждой из четырех точек можно вычислять на отдельном процессоре.
Выражения, по которым вычисляются приращения в четырехточечном блоке, имеют следующий вид:
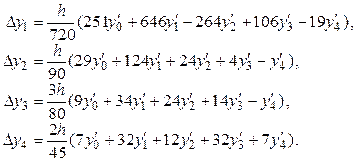 (2.15)
(2.15)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.