Параллельное программирование: Учебное пособие, страница 30

Рисунок 2.10б для расматриваемой задачи с 11 взаимодействующими блоками дает идеальную картину размещения параллельных процессов во времени. Здесь предполагается, что межярусный временной интервал выбран таким образом, чтобы все вершинные процессы одного яруса до обмена данными были закончены. Кроме того, зачастую обнаруживается важный факт относительно степени параллелизма, как, например, в названном рисунке 2.10б. Параллелизм на том или ином ярусе в некоторых случаях может быть изменен. Например, вершину 5 (е) на рисунке 2.10б можно переместить со второго яруса на третий, а вершину 6 (f) – c третьего на четвертый. Этими перемещениями мы можем добиться того, что на всех ярусах степень параллелизма не превысит два.

Однако есть и существенные недостатки в таком упорядочении. Оно проведено в предположении того, что все вершинные процессы длятся одинаковое время, чего реально при разбивке задачи на блоки добиться не удается. Отличаться эти времена друг от друга могут в несколько раз. Поэтому задачу подвижки отдельных вершин в пределах допустимых для них ярусов нужно решать с учетом такого параметра вершины, как длительность вершинного процесса.

2.3.5  Учет времени протекания вершинных процессов.

Блоки задачи, сформированные для их параллельного выполнения, должны представлять по возможности законченные алгоритмы, которые используют для своего преобразования только априорно заданные значения и значения, переданные в момент запуска блока. Если алгоритмы блоков представлены готовыми текстами программы, то в процессе компиляции и тестирования их контрольными примерами можно в удобных единицах оценить истинное время протекания вычислительного процесса каждого выделенного блока. Желательно, чтобы погрешность оценок времени составляла не более 10%.

Временные оценки длительности вершинных процессов не должны превышать по длительности межярусный промежуток. Ведь каждый ярус после упорядочения графа определяет момент запуска (по готовности данных) процессов в вершинах, расположенных на более поздних ярусах дальше, и увеличение длительности вершинного процесса может привести к переориентации некоторых дуг графа и в первую очередь той, которая исходит от вершины, затянувшей процесс. Поэтому условием выбора длительности интервала между ярусами (и не обязательно одинаковой со всеми) должно быть превышение этой длительности над длительностью наиболее длинного процесса на ярусе:

,                                                        (2.27)

где      время выполнения k-того процесса на j-том ярусе.

В качестве примера на рис. 2.13 изображен упорядоченный по ярусам граф рисунка 2.10, в котором на месте вершин изображены отрезки с длинами, пропорциональными длительности процесса в вершине.

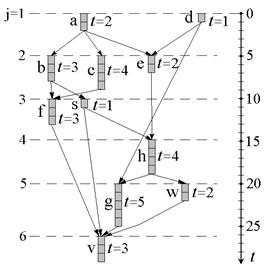Рисунок 2.13.

Показанная справа шкала относительного времени, к которой привязаны ярусы, дает представление о таких перемещениях ярусов, которые не изменили бы на обратное направление проекций дуг на временную ось. По разметке и с учетом (2.27) легко увидеть перемещение ярусов на такие отметки:

ярус 2 ® отм.2;   я.3 ® 6;       я.4 ® 9;       я.5 ® 13;    я.6 ® 18.

Однако такое очевидное распределение во времени с синхронным запуском вершинных процессов, находящихся на одном ярусе, не решает еще, по крайней мере, двух противоречивых проблем: минимизации числа процессоров,  необходимого  для решения  задачи  за минимальное  время, и

минимизации времени решения задачи на заданном числе процессоров. Первая проблема упирается в необходимость перемещения вершин с яруса на ярус вверх и вниз так, чтобы, не меняя направления проекций дуг на временную ось, максимально сблизить последовательно выполняемые процессы, после чего выбрать число процессоров по максимальной степени параллелизма полученного графа информационной зависимости. Вторая проблема связана с принудительным контролируемым перемещением отдельных процессов по оси времени (по ярусам) так, чтобы степень параллелизма не превысила числа заданного количества процессоров.