Параллельное программирование: Учебное пособие, страница 21

Чтобы получить шестой порядок погрешности необходимо для каждого приращения выполнить по четыре итерации. На каждом процессоре (по аналогии с предыдущим примером) должны сначала по формуле Эйлера вычисляться значения функции, по которым в этой же точке вычисляется первое приближенное значение производной. По собранным с остальных процессоров первым приближениям производных вычисляется приращение функции и новое значение самой функции. По окончании итераций вычисленные значения либо накапливаются в каждом процессоре с шагом 4h, либо после каждого цикла передаются на сборку всего переходного процесса в главный (ведущий) процессор.

2.2.5  Распараллеливание циклов.

Рассмотренные выше подходы к распараллеливанию касались таких участков вычислений, которые давали возможность повысить ускорение за счет существенного увеличения числа процессоров, однако при этом эффективность использования процессоров (загрузка полезной работой) в такой же степени снижалась. При этом, как правило, отмечался рост числа дополнительных или дублируемых операций, а ускорение редко достигало удвоенного значения по сравнению с лучшими последовательными алгоритмами. Поэтому следует обратить особое внимание на те участки вычислений и программ, в которых “скрыт” основной потенциальный параллелизм. Такими участками являются, например, простые и многомерные циклы (гнезда вложенных друг в друга простых циклов):

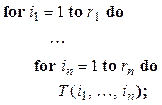                                                                              (2.16)

В псевдокоде многократно повторяющейся вычислительной процедуре, называемой телом цикла , параметры  являются индексами (номерами) элементов массивных (многомерных) переменных, которые являются операндами вычислительных конструкций тела. Диапазон изменения индекса каждого элемента обычно приводят к диапазону чисел натурального ряда  с единичным шагом. Если оператор цикла в языковой конструкции в общем случае представлен как

,                                            (2.17)

где      – соответственно выражения для получения целочисленных значений переменной цикла, ее начальной границы, конечной границы и шага, то введением новой индексной переменной i и заменой  в  получим оператор цикла требуемого вида:

 .                                                            (2.18)

Здесь индекс переменной i изменяется уже с единичным шагом от единицы до верхнего граничного значения .

Относительно тела цикла  в одномерном случае или  в многомерном случае предполагается, что величины  вычисляются до входа в цикл и не изменяются телом цикла, вычисление операторов тела для всех значений индексов обязательно, в любом проходе цикла не может быть отсылок за его пределы, а во вложенных циклах – и из любого внутреннего.

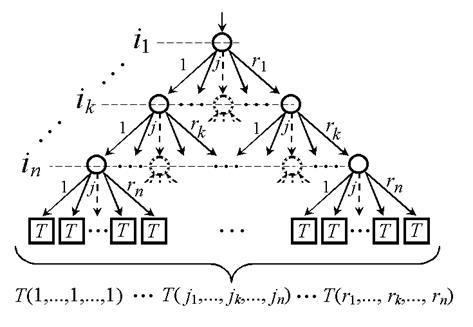На рисунке 2.8 изображена картина прохождения всех итераций цикла. Общее число прохождений тела цикла равно произведению верхних границ всех индексных переменных: . Внутренний цикл во вложенной структуре многомерного цикла изменяет свою индексную переменную чаще, чем внешний цикл изменяет свою индексную переменную.

Рассматривая структуру прохождения тела в пределах индексного множества, можно высказать ряд соображений относительно типов обработки и преобразования структурных данных и области, над которой производится вычисление.

В любом теле цикла последовательность операторов обязательно перерабатывает некоторый набор исходных данных в определенный набор выходных данных. Эти наборы данных могут быть, как минимум, двух типов: простыми или/и индексными переменными, и тем самым определять, например, следующие четыре типа циклических вычислений.

–  Скаляр ® скаляр:  () – поток значений входной переменной  преобразуется телом цикла Т в поток значений выходной переменной . Индексное множество, как таковое, здесь принципиальной роли не играет. Такой порядок вычислений эквивалентен некоторой нециклической конструкции, например, вычислению значений по рекуррентным или итерационным формулам. В языковых конструкциях такие вычисления обычно представляются в форме