Прямое произведение двух упорядоченных множеств А и В равно множеству всех упорядоченных пар, в которых первый элемент пары принадлежит А, а второй принадлежит В:
![]() .
.
Всего в этом произведении будет ![]() упорядоченных пар. Если возводится во
вторую степень упорядоченное множество в виде
упорядоченных пар. Если возводится во
вторую степень упорядоченное множество в виде ![]() -матрицы,
заполненной элементами двух значений
-матрицы,
заполненной элементами двух значений ![]() , то приписывая
поочередно к некоторому элементу
, то приписывая
поочередно к некоторому элементу ![]() i-той
строки первой
i-той
строки первой ![]() -матрицы каждый из элементов j-го столбца второй
-матрицы каждый из элементов j-го столбца второй ![]() -матрицы,
будем получать ij-тое множество пар четырех видов {
-матрицы,
будем получать ij-тое множество пар четырех видов {![]() }. Первые три пары указывают на то, что
отношения смежности между вершинами
}. Первые три пары указывают на то, что
отношения смежности между вершинами ![]() нет и эти пары
можно заменить одним значением 0, а последняя пара характеризует сохранение
смежности вершин, которую можно обозначить единицей. Такую замену можно
выполнять по правилам булевой алгебры с помощью операции конъюнкции (
нет и эти пары
можно заменить одним значением 0, а последняя пара характеризует сохранение
смежности вершин, которую можно обозначить единицей. Такую замену можно
выполнять по правилам булевой алгебры с помощью операции конъюнкции (![]() ). Выполняя дизъюнкцию между парами ij-того
множества, мы можем получить ответ: есть ли хотя бы одно отношение смежности
между вершинами i-той строки и j-го столбца? Всякое очередное увеличение степени
отношений смежности будет отвечать на вопрос: сохранен ли путь между вершинами,
удлиненный еще на одну дугу? Объединение всех степеней позволит ответить на
вопрос о существовании пути из одной вершины в другую.
). Выполняя дизъюнкцию между парами ij-того
множества, мы можем получить ответ: есть ли хотя бы одно отношение смежности
между вершинами i-той строки и j-го столбца? Всякое очередное увеличение степени
отношений смежности будет отвечать на вопрос: сохранен ли путь между вершинами,
удлиненный еще на одну дугу? Объединение всех степеней позволит ответить на
вопрос о существовании пути из одной вершины в другую.
Для вычисления транзитивного замыкания используют известный алгоритм Уоршалла сложности n3 с тремя вложенными циклами перебора строчных и столбцовых индексов:
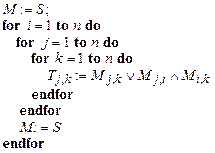 (2.26)
(2.26)
В результате возведения матрицы
смежности ![]() в n-ную
степень с логическими операциями
в n-ную
степень с логическими операциями ![]() -й элемент матрицы
-й элемент матрицы ![]() будет равен
будет равен
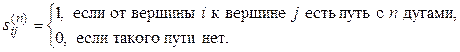
Объединение же всех n степеней покажет наличие в графе всех путей с длинами от одного до n шагов (по числу дуг).
Если же (0,1)-матрицу смежности
возвести в n-ную степень по правилам умножения
матриц со скалярной арифметикой, то единица на пересечении i-той
строки и j-го столбца будет свидетельствовать о
наличии пути длиною n, а сумма всех степеней будет указывать на
максимальное расстояние (число дуг) от вершины ![]() до вершины
до вершины
![]() .
.
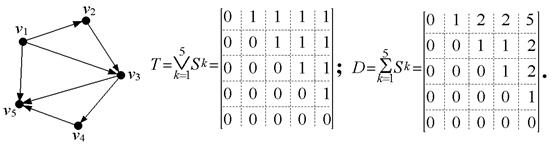
По матрице смежности графа,
показанного на рисунке 2.9, с помощью алгоритма Уоршалла (2.26) получена
матрица транзитивного замыкания Т и по формуле 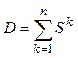 вычислена матрица максимальных
расстояний.
вычислена матрица максимальных
расстояний.
 |
В произвольно составленной матрице смежности орграфа множеству имен вершин можно придать транзитивное свойство. Для этого достаточно поместить каждое имя вершины в информационную часть элемента индексного списка. В этом случае к имени вершины можно обращаться по индексу, представленному числом натурального ряда. Упорядоченный по индексу список вершин предстанет множеством новых имен вершин орграфа. Однако для параллельных форм алгоритмов важно, чтобы транзитивное свойство зерен-вершин, определяемое возрастанием их индекса, было согласовано с направлением перехода от вершины к вершине по дугам. Это позволит выстроить все множество вершин орграфа в такой последовательности, когда все зерна-вершины параллельной формы алгоритма будут передавать подготовленные данные только вершинам с большим индексом. Натуральные числа индексов в первом приближении будут характеризовать временную последовательность включения очередного оператора, закрепленного за именем вершины. Именно эту задачу мы решали эвристически, создавая ярусные параллельные формы для регулярных фрагментов. Теперь же необходимо построить ярусную форму по орграфу задачи с нерегулярной структурой взаимодействующих друг с другом вычислительных фрагментов. Для достижения этой цели надо провести сортировку (переиндексацию) имен вершин в списке так, чтобы их упорядоченное расположение соответствовало направлениям дуг.
Свяжем с каждой вершиной ![]() в
списке два подмножества вершин (при необходимости в виде двух списков). Одно
подмножество с мощностью, равной отрицательной полустепени
в
списке два подмножества вершин (при необходимости в виде двух списков). Одно
подмножество с мощностью, равной отрицательной полустепени ![]() , включает имена вершин, от которых дуги
приходят к
, включает имена вершин, от которых дуги
приходят к ![]() , и второе подмножество с мощностью, равной
положительной полустепени
, и второе подмножество с мощностью, равной
положительной полустепени ![]() , включает имена вершин,
на которые дуги направлены от
, включает имена вершин,
на которые дуги направлены от ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.