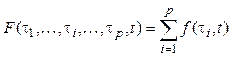Параллельное программирование: Учебное пособие, страница 33

.                                                           (2.31)

На рисунке 2.16а по параметрам графа информационной зависимости, занесенным в таблицу 2, приведены отрезки единичных функций для каждой вершины. Отрезки над осью времени придвинуты к началу координат до границ ранних сроков окончания вершинных процессов , а под осью – к границам поздних сроков окончания . Пунктирные отрезки единичных функций показывают возможность помещения отрезка между левой и правой границами.

Суммы всех единичных отрезков функций, приведенные на рисунке 2.16б и 2.16г, соответствуют функциям плотности загрузки параллельной вычислительной системы, если руководствоваться при запуске вычислений соответственно только левыми или только правыми границами окончания вершинных процессов. На этих функциях хорошо видно, что вычислительная система в отдельные моменты времени вынуждена включать в работу то один, то два, то три процессорных устройства.

Перемещая тем или иным образом подвижные вершинные процессы, например, показанные пунктирно на рисунке 2.16а, и вычисляя функцию плотности загрузки, можно добиться использования в любой момент меньшего числа процессорных устройств. Один из возможных вариантов размещения  этих  процессов, приведенный  на рисунке 2.16а,  дает  функцию плотности загрузки, показанную на рисунке 2.16в, где используется для вычислений всего два процессора.

Объем вычислительных работ, произведенный системой в течение некоторого отрезка времени , можно вычислить путем интегрирования по времени функции плотности загрузки:

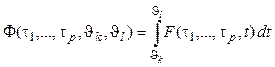.                                                 (2.32)

Функция загрузки интервала  является функцией значений ,  и может принимать множество значений, определяемых видом функции плотности загрузки в выбранном интервале. Из множества значений функции загрузки интервала  выберем наименьшее значение, назвав его функцией минимальной загрузки:

,                                (2.33)

где     момент окончания i-того процесса.

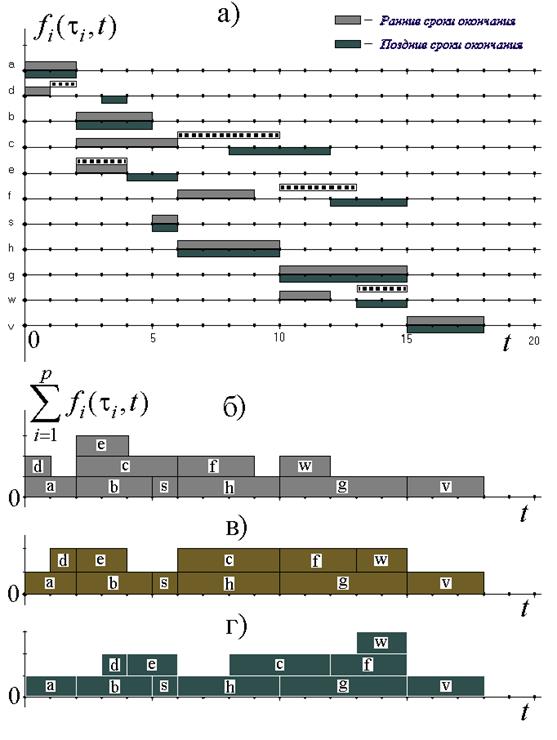Рисунок 2.16.

При данном  и допустимых значениях множества времен окончания процессов {} функция минимальной загрузки определяет минимально возможный объем работ, который может быть выполнен в течение интервала .

Чтобы  было наименьшим временем выполнения данного алгоритма с  процессорами, либо чтобы  процессоров было достаточно для его выполнения, необходимо, чтобы для данного отрезка  было справедливо соотношение

                                                     (2.34)

или  

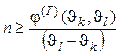.                                                                  (2.35)

Правая часть (2.34) представляет площадь прямоугольника, вычисленную на интервале , если функция плотности загрузки на нем была бы постоянной и равной числу одновременно выполняемых процессов. Левая же часть соответствует функции загрузки этого интервала, то есть площади фигуры, ограниченной сверху кривой функции плотности. Очевидно, что объем вычислительных работ, представленный левой частью (2.34), должен быть меньше или равным максимально возможному объему работ для n процессоров. Однако для сохранения Т или n на минимальном значении условия (2.34, 2.35) недостаточно, так как возможны случаи, когда в рассматриваемом интервале  некоторые перемещения процессов невозможны, а некоторые не приводят к изменению объема вычислений.

Перемещаемые процессы могут изменять свое положение лишь в границах раннего  и позднего  сроков своего окончания. При этом могут возникнуть ситуации, в которых для выбранного интервала  невозможно хотя бы частично выполнить смещение отрезка единичной функции вершины либо их перемещение ничего не изменяет. К ним можно отнести, например, процессы начала и конца параллельного алгоритма и частично процессы, определяющие критическое время алгоритма.

Объемы выполняемых работ в интервале  будут изменяться при перемещениях процессов лишь в тех случаях, когда длительность перемещаемого процесса будет покрывать выбранный интервал частично. Отрезок совместного перекрытия можно выразить импульсной пороговой функцией с амплитудой, определяемой аргументом, значение которого равно длительности перекрытия двух интервалов: