Параллельное программирование: Учебное пособие, страница 26

Аналитическое описание графа G включает непустое множество вершин , множество дуг , не пересекающееся с , и отображение  множества  на .  называется ориентированным отображением инцидентных вершин орграфа. Если , то  означает, что дуга  имеет начальную вершину  и конечную вершину . Таким образом, орграф вводится тройкой параметров и обозначается как .

Граф называется помеченным, если за каждым его элементом закреплено оригинальное обозначение, например, для вершин  и  – для ребер. Специальная индексация элементов числами натурального ряда позволяет в общем провести такую разметку вершин, которая установит отношение порядка на элементах множеств. Это важно для временного распределения действий в параллельных ветвях программы.

Отношение порядка – бинарное отношение R (binary relation), обладающее свойствами антирефлексивности (antireflexivity – без отражения на самого себя) и транзитивности (transitiveness – переходность, строгая упорядоченность). Это отношение обозначают символами    в зависимости от типов объектов, для которых это отношение вводится: для чисел, для множеств, для алгебраических структур.

Антирефлексивность – свойство бинарного отношения, при котором в заданном множестве не найдется элемента x такого, чтобы было . То есть

для отношения порядка не существует элемента  или .

Транзитивность – свойство бинарного отношения R такое, что для элементов  заданного множества всегда следует, если  и . Для отношения порядка свойство транзитивности означает, что, если  и , то .

Названное отношение порядка для орграфа полностью соответствует исходным отношениям между зернами и информационными потоками параллельных форм, получаемых на основе математической постановки распараллеливаемой задачи. Это позволяет успешно использовать весь арсенал формальных преобразований орграфов для целей построения параллельных программ на заданном числе процессоров.

Для определения множества вершин орграфа по параллельной форме алгоритма достаточно включить в это множество имена всех зерен формы. Аналогично в множество ориентированных дуг нужно включить имена всех стрелок, которые закреплены за ориентированными дугами. Формальное отображение множества дуг на множество вершин можно задать несколькими способами. Например, множеством с элементами в виде инцидентных пар вершин, связанных одной дугой, или множеством с элементами в виде инцидентных пар вершина-дуга. Использование инцидентных пар в качестве аналитического определения орграфа для последующей машинной обработки наиболее популярно в виде матрицы смежности, матрицы инциденций или развернутой тройки помеченного орграфа. Они являются упорядоченными множествами отношений.

Матрица смежности  помеченного орграфа  с  вершинами есть ()-матрица, в которой

, если дуга  ,

, если дуга ,

где     i перечисляет вершины, из которых направленная дуга выходит, а

j перечисляет вершины, в которые дуга входит, например:

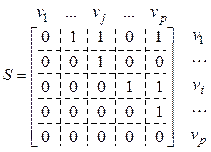                                            (2.21)

Матрица инциденций  помеченного орграфа с  вершинами и  ребрами есть -матрица с элементами .

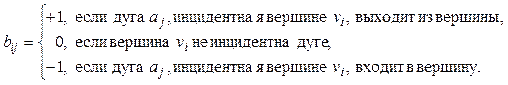
Дуги  перечисляются в матрице по столбцам, а вершины  перечисляются по строкам, например:

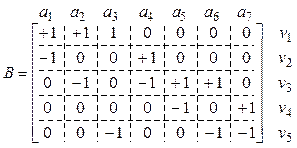                                  (2.22)

Граф , заданный тремя множествами, например, множеством инцидентных вершин , множеством ребер  и множеством отображений ориентированных дуг на инцидентные вершины.

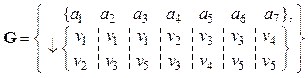.                              (2.23)

Отметим следующие важные понятия и определения для орграфов.

Если в связном графе нет циклов, его называют деревом. Граф связен, если множество его вершин нельзя разбить на два непустых подмножества  так, что обе граничные точки каждого ребра находятся в  или .

Конечная последовательность различных дуг () называется цепью (путем), если существует следующая последовательность пар инцидентных вершин:  . Цепь длины n является последовательностью дуг, соединяющих () вершину орграфа. Замкнутая цепь называется циклом (контуром). В рассмотренных выше параллельных формах циклы (контуры) из рассмотрения заведомо исключались. Однако замкнутые цепи больших длин в сложных задачах могут возникнуть в результате ошибок программиста. Граф сильно связный, если для каждой пары вершин  u  и  v  существует путь из  u  в  v  и из  v  в  u.