Параллельное программирование: Учебное пособие, страница 32

Следовательно, задачу поиска поздних сроков необходимо решать, следуя условию реализации всего вычислительного процесса за минимально возможное время, не обращая пока внимания на реализуемость максимальной степени параллелизма. Минимально же возможное время уже получено благодаря исполнению алгоритма рисунка. 2.14.

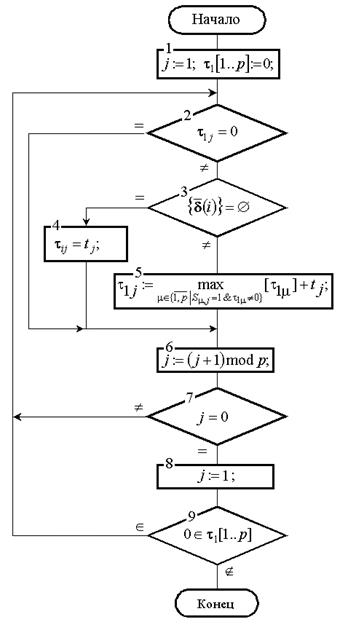Рисунок 2.14.

В нем все процессы были максимально близко придвинуты к началу всего параллельного вычислительного процесса, поэтому ранний срок окончания самого последнего вершинного процесса на самом нижнем ярусе определяет минимальное время выполнения всего параллельного процесса. Это время называют критическим временем , так как оно складывается из суммы времен исполнения вершинных процессов, привязанных к вершинам лежащим на самом длинном по времени критическом пути взвешенного графа информационной зависимости. При всем желании выполнить параллельный алгоритм за меньшее время принципиально невозможно.

В пределах критического времени можно теперь найти и наиболее поздние сроки окончания вершинных процессов путем подтягивания их как можно ближе к , не нарушая направленности проекций дуг критических путей графа на временную ось. Эту задачу можно решить с помощью алгоритма рисунка 2.15, который подобен алгоритму поиска ранних сроков. Отличие состоит в организации просмотра вершин от самой поздней по исполнению к самой ранней в ГИЗ и использованию другой формулы вычисления позднего срока окончания вершинного процесса:

.                                                   (2.29)

где      поздние сроки окончания процессов -тых вершин для заданного общего времени вычислений . Минимум выбирается из -тых разностей, для которых одновременно выполнено условие, что на -том столбце -й строки матрицы смежности  находится единица и для -той строки колонки  таблицы 2 поздний срок окончания уже найден.

Просмотр строк в матрице смежности и таблице 2 начинается с последней строки . Если для вершины, лежащей на -той строке, поздний срок окончания еще не вычислялся, то есть , то проверяется наличие выходящих дуг: пуста ли положительная полустепень вершины {Æ}?  Если выходящих дуг нет, то позднее время окончания процесса приравнивается максимальному времени  выполнения параллельного алгоритма, в противном случае это время вычисляется по (2.29).

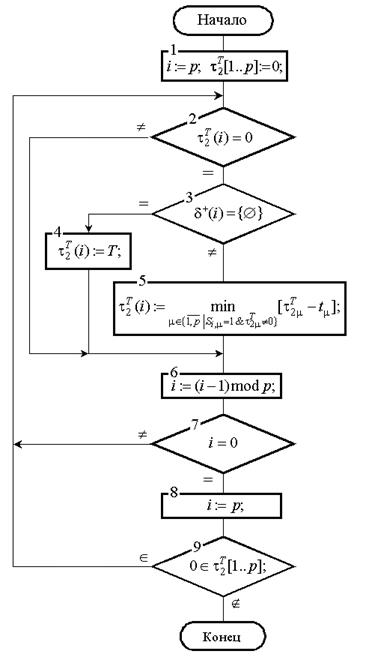Рисунок 2.15.

В таблице 2 в двух крайних колонках справа вписаны ранние и поздние сроки окончания вершинных процессов. Для каждой вершины эти значения являются границами, в которых можно перемещать во времени моменты окончания вершинного процесса или, вычтя его длительность, – моменты запуска процесса. Если поздние сроки окончания вершинных процессов вычислялись при , то на i-тых строках в таблице 2 значения  и окажутся равными. Эти вершинные процессы не могут быть перемещены во времени. Нетрудно заметить, что при  разность сроков окончания процессов будет равна . Эту зависимость можно использовать для контролируемого понижения средней степени параллелизма путем увеличения времени выполнения всего параллельного алгоритма.

Появление свободы в выборе моментов запуска вершинных процессов позволяет поставить задачу такого размещения процессов в ограниченном интервале времени, чтобы степень параллелизма оказалась минимально возможной. Для задачи оптимального размещения необходимо получить аналитическое выражение функционала, минимизация которого привела бы к нужному результату.

2.3.7  Оптимизация размещения процессов в алгоритме

Представим протяженность каждого i-того вершинного процесса на временной оси в виде отрезка единичной функции

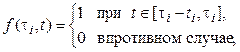                                                          (2.30)

где     текущее время выполнения алгоритма в интервале от 0 до ;

           длительность выполнения i-того процесса;

           время окончания выполнения i-того процесса.

Просуммировав отрезки единичных функций вершинных процессов, получим аналитическое выражение функции плотности загрузки параллельно работающих процессоров в любой момент времени :