Если в не связном графе ![]() все его подграфы
все его подграфы ![]() не
содержат циклов, то граф с деревьями подграфов
не
содержат циклов, то граф с деревьями подграфов ![]() называют
лесом.
называют
лесом.
Каждое дерево с n
вершинами имеет в точности (![]() ) ребро, а лес с n
вершинами и k деревьями – в точности (
) ребро, а лес с n
вершинами и k деревьями – в точности (![]() ) ребер.
) ребер.
Число ребер, инцидентных вершине ![]() , называют степенью вершины
, называют степенью вершины ![]() и обозначают как
и обозначают как ![]() .
Для изолированной вершины
.
Для изолированной вершины ![]() степень вершины
степень вершины ![]() , а для вершины орграфа
, а для вершины орграфа ![]() , где слагаемые с верхними индексами
обозначают соответственно положительную и отрицательную степени вершины
, где слагаемые с верхними индексами
обозначают соответственно положительную и отрицательную степени вершины ![]() , т.е. число дуг выходящих из вершины и
число входящих соответственно. Общее число дуг
, т.е. число дуг выходящих из вершины и
число входящих соответственно. Общее число дуг ![]() в
орграфе равно
в
орграфе равно
![]()
![]() . (2.24)
. (2.24)
Согласно рассмотренным параллельным формам все операторы размещены так, что последовательность их включения следует строгому порядку, то есть, глядя на нее, можем уверенно сказать, какой из операторов должен включиться на исполнение раньше другого, лежащего на одном пути. Следовательно, и в упорядоченной последовательности вершин орграфа, представляющего параллельную форму, начальная вершина любого пути должна находиться раньше конечной. Поэтому первоначальной задачей теоретического анализа и преобразования орграфа является такая его разметка, которая обеспечит эту строгую упорядоченность.
В ациклическом (без контуров)
орграфе с дугами ![]() всегда можно пометить вершины
всегда можно пометить вершины ![]() одним индексом
одним индексом ![]() так,
что
так,
что ![]() . Расстоянием между вершинами служит число
дуг, находящихся на пути, связывающем эти вершины. Путь от начальной вершины
орграфа до конечной вершины орграфа, содержащий наименьшее число дуг, называют критическим
путем. Минимальное число индексов
. Расстоянием между вершинами служит число
дуг, находящихся на пути, связывающем эти вершины. Путь от начальной вершины
орграфа до конечной вершины орграфа, содержащий наименьшее число дуг, называют критическим
путем. Минимальное число индексов ![]() на
единицу больше длины критического пути. Приведение разметки к указанному виду
называют топологической сортировкой. Топологическая сортировка
называется линейной, если индексы любых вершин различны.
на
единицу больше длины критического пути. Приведение разметки к указанному виду
называют топологической сортировкой. Топологическая сортировка
называется линейной, если индексы любых вершин различны.
Два графа изоморфны, если между их множествами вершин и дуг можно установить взаимно однозначное соответствие, сохраняющее смежность и ориентацию.
Гомоморфизм – унарная операция на графе. Замена по определенным правилам некоторого множества вершин и дуг одной новой вершиной. Элементарным гомоморфизмом графа называется отождествление двух его смежных вершин. Операцию гомоморфизма можно трактовать как процесс слияния вершин с непрерывным изменением всех связанных с ними дуг с последующим исключением петель и отождествлением кратных ребер. Последовательность гомоморфного преобразования графа называется сверткой графа.
Объединение графов:
![]() .
.
Пересечение графов:
![]() .
.
Начальными вершинами являются те вершины, столбцы матрицы смежности которой являются нулевыми.
Конечными вершинами являются те вершины, строки матрицы смежности которой являются нулевыми.
В орграфе без петель с матрицей смежности S контуры отсутствуют тогда и только тогда, когда существует матрица перестановок Р такая, что матрица из произведений Рт S Р является нижней треугольной.
Сумма элементов в ![]() -й строке матрицы смежностей равна числу
выходящих дуг из вершины
-й строке матрицы смежностей равна числу
выходящих дуг из вершины ![]() , то есть положительная
степень вершины равна
, то есть положительная
степень вершины равна ![]() (полу степень исхода), а сумма
элементов в
(полу степень исхода), а сумма
элементов в ![]() -том столбце матрицы смежностей равна числу
входящих в
-том столбце матрицы смежностей равна числу
входящих в ![]() вершину дуг, то есть отрицательной степени
вершины
вершину дуг, то есть отрицательной степени
вершины ![]() (полу степень захода).
(полу степень захода).
Транзитивное замыкание
отношения – бинарное отношение ![]() , определенное как
объединение всех степеней данного бинарного отношения
, определенное как
объединение всех степеней данного бинарного отношения ![]() :
:
![]() тогда и только тогда, когда найдется такое
тогда и только тогда, когда найдется такое
![]() , что
, что ![]() .
.
Транзитивное замыкание ![]() для
отношения
для
отношения ![]() на матрице смежности
на матрице смежности ![]() , состоящее в том, что две вершины
, состоящее в том, что две вершины ![]() и
и ![]() соединены
дугой (
соединены
дугой (![]() ,
,![]() ), то есть
), то есть ![]() , является отношением достижимости на
орграфе вершины
, является отношением достижимости на
орграфе вершины ![]() от вершины
от вершины ![]() , то есть
, то есть ![]() .
Построение матрицы достижимости
.
Построение матрицы достижимости ![]() , которая показывает,
есть ли путь от
, которая показывает,
есть ли путь от ![]() к
к ![]() ,
осуществляется по матричному выражению с булевскими операциями:
,
осуществляется по матричному выражению с булевскими операциями:
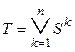 , (2.25)
, (2.25)
где ![]() – упорядоченное
множество отношений между вершинами, представленное, например,
– упорядоченное
множество отношений между вершинами, представленное, например, ![]() -матрицей смежности;
-матрицей смежности;
![]() –
степень множества, равная прямому произведению множества
–
степень множества, равная прямому произведению множества ![]() на само себя. k-тая степень
соответствует прямому произведению k множеств
на само себя. k-тая степень
соответствует прямому произведению k множеств ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.