Параллельное программирование: Учебное пособие, страница 29

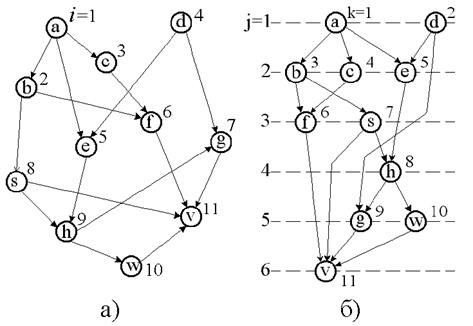
В качестве примера такого списка может служить приведенная ниже таблица 1 с несколькими столбцами, составленная по графу информационной зависимости, приведенному на рисунке 2.10а.

Таблица 1.  Список вершин с множествами дуг (выходных/входных).

Для лексикографического упорядочения орграфа удобно использовать колонку  таблицы 1. В таблицу введены два дополнительных столбца: один предназначен для закрепления за вершиной  порядкового номера яруса j , а второй – для записи нового упорядочивающего индекса .

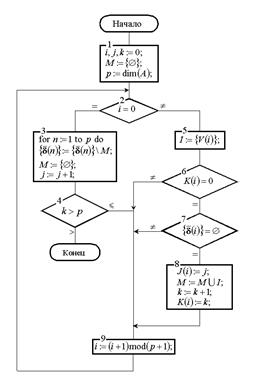
Алгоритм, показанный на рисунке 2.11, размещает вершины по ярусам и присваивает им новые индексы. В результате множество вершин будет упорядочено так, что между его элементами будет иметь место отношение порядка: , если , где . В операторах схемы рис. 2.11 использованы такие выражения и обозначения:                                                      Рисунок 2.11.

число вершин орграфа;

исходный индекс, ярус и новый индекс вершины орграфа;

множество вершин от которых входят дуги;

рабочее множество вершин, исключаемых из .

Матрица смежности для графа, представленного рисунком 2.10, до и после лексикографического упорядочения приведена на рисунке 2.12.

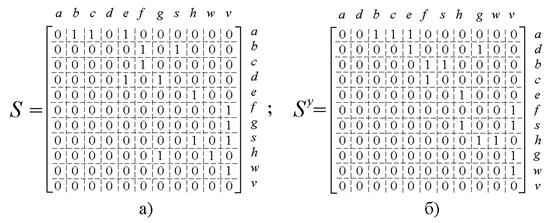Рисунок 2.12.

Смысл лексикографического упорядочения удобно описать, используя визуальное или табличное представление орграфа следующим образом:

По именам {a, b, c,...} или по их первоначальным индексам {1, 2, 3,...} в списке (колонки Т(2), Т(1) в таблице 1) последовательно просматриваются отрицательные полустепени вершин  (колонка Т(4)). Вершины, удовлетворяющие условиям  (новый индекс имени еще не присвоен) и Æ  (нет входящих дуг), помещаются в рабочее множество М с присвоением им одного и того же номера яруса ( ) и очередного индекса вершины () . В конце очередного цикла индексная переменная  принимает значение , которое запускает процесс исключения из всех множеств  тех вершин, которые были занесены в рабочее множество (М) . При этом исключении появятся новые вершины, у которых отсутствуют входящие дуги. Вершины, которым ранее уже был присвоен новый индекс и для них  , в очередном цикле пропускаются, а вершины с отрицательной полустепенью равной нулю, помещаются в рабочее множество вершин нового яруса. Циклы просмотра продолжают до тех пор, пока всем вершинам не присвоят новые индексы.

Расположив вершины по своим ярусам по возрастанию нового индекса слева направо и сверху вниз, получим граф, показанный на рисунке 2.10б, и его верхнетреугольную упорядоченную матрицу смежности (Рис. 2.12б).