Независимо от того, как скомпонованы параллельные вычислительные системы, все они в каждый момент времени одновременно на всех процессорах могут или осуществляют преобразование информации в своем ритме и, до поры до времени, независимо друг от друга. Единственная алгоритмическая причина, по которой каждый из группы процессов может приостановить свое функционирование, это необходимость обратиться к области памяти с данными, состояние которых определяется частью или всеми процессами параллельного алгоритма. Поэтому, чтобы параллельный алгоритм мог быть реализован для исполнения на параллельной вычислительной системе, его предварительно необходимо представить в виде множества обособленных зерен, то есть групп связанных операторов и операций, выступающих как цельное образование с одной точкой запуска запрограммированных действий и одной точкой выхода при их завершении.
Наглядным примером такой группы операций ориентировочно может служить процедура, подпрограмма, функция, блок или вся решаемая задача, описанные на языке программирования. На момент запуска в группе вычислительного процесса в точку входа передаются параметры, однозначно идентифицирующие место положения и характеристику подготовленных к использованию данных. Результатом завершения таких групп операций является изменение состояния некоторых внешних, то есть доступных для других процессов, данных. Не вдаваясь в подробности исполнения и языковое описание таких групп, эти образования для последующего анализа параллельной задачи достаточно именовать любым удобным для отображения способом, приписывая или придавая им при необходимости количественные параметры. Для графического изображения процессов в таких образованиях (зернах) можно использовать какую-либо плоскую фигуру, в которую входят и уходят стрелки от и на аналогичные графические фигуры. Входящие стрелки исходят от тех фигур, которые изображают процессы, подготавливающие данные изображенному процессу, а выходящие – приходят к изображениям процессов, которые будут потреблять преобразованные данные [1]. На рисунке 2.1 показан фрагмент такого изображения взаимосвязанных процессов. Кружочки – это отрезки процессов (thread), стрелки – пути взаимодействия (interaction) посредством передачи данных. Каждый из названных объектов характеризуется, как минимум, одним параметром – длительностью.
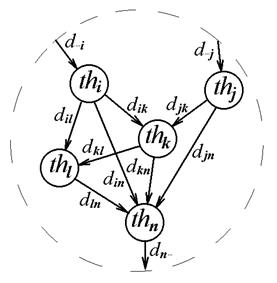 |
Рисунок 2.1.
Представление алгоритма в подобном виде называют параллельной формой алгоритма. Каждый отрезок процесса называют ярусом параллельной формы, число отрезков процессов – высотой параллельной формы, а максимальное число процессов в ярусе – шириной параллельной формы.
По известной параллельной форме алгоритма можно реализовать и сам алгоритм, например, последовательно по ярусам выполняя все отрезки процессов, для которых данные будут уже подготовлены предыдущими ярусами. Такой тривиальный подход к выполнению алгоритма по заданной параллельной форме для одного процессора используется всеми программистами с первых дней появления машин фон-неймановской структуры.
Однако если имеются вычислительные и коммуникационные средства со многими процессорами, то, наверное, можно выделить такие группы процессов, которые будут выполняться параллельно и одновременно на разных процессорах. Такая задача выделения параллельных групп процессов в большинстве случаев нетривиальна. Ее решение может иметь множество параллельных форм, различающихся и высотой и шириной.
Наиболее привлекательными среди параллельных форм являются формы минимальной высоты. Именно такие формы параллельных алгоритмов, которые строятся, руководствуясь принципом неограниченного параллелизма, возможно, позволят провести вычисления за наименьшее время. Поиск максимальных параллельных форм, хоть и приводит к неким гипотетическим вычислительным структурам, однако подбрасывает “пищу” и для глубоких размышлений.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.