Параллельное программирование: Учебное пособие, страница 11

Степенью параллелизма вычислительного алгоритма называют число операций, которые можно выполнять параллельно.

В каждый момент развертывания параллельного вычислительного процесса степень параллелизма может изменяться от единицы (выполняется один процесс) до некоторого числа , определяемого конкретной задачей и ограничиваемого числом имеющихся процессоров.

Средней степенью параллелизма называют отношение общего числа операций (точнее – процессов) на всех дискретных отрезках времени к общему числу дискретных интервалов, в сумме представляющих полное время выполнения параллельных процессов.

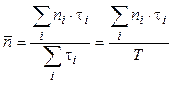,                                                                (1.1)

где      – число процессов (или операций) на  -том отрезке времени;

            – длительность интервала, на котором ;

            – время выполнения параллельного алгоритма.

Если на протяжении всего алгоритма , то .

1.8  Формальная модель ускорения алгоритмов

В разделе 1.6 приведено определение ускорения параллельного алгоритма по сравнению с вычислением этого алгоритма на одном процессоре. В знаменателе отношения времен находится время вычисления параллельного алгоритма. Оценка этого времени может быть проведена с использованием длительностей отдельных параллельно идущих процессов и степеней параллелизма в каждый текущий момент дискретного времени. В литературе модель ускорения часто рассматривается для случая, когда все операции в параллельных процессах одинаковы по длительности. Зернистость исходной задачи, определяющая отдельные фрагменты параллельно идущих процессов, в большинстве случаев не позволяет считать длительности этих фрагментов одинаковыми. Поэтому формула модели ускорения должна быть несколько модифицирована с учетом данных выше определений степени параллелизма и средней степени параллелизма.

Можно считать, что весь параллельный алгоритм исполняется в дискретные моменты времени . В каждый такой момент на одинаковых интервалах  в режиме выполнения могут одновременно находиться от одного до  процессов.

На рисунке 1.3 показан возможный фрагмент параллельного алгоритма, где окрашенными отрезками обозначены процессы, которые последовательно выполняются на  процессорах.

На всем протяжении параллельного алгоритма можно сложить элементарные вычислительные отрезки с одной и той же степенью параллелизма. Тогда длительность вычислений со степенью параллелизма  будет равна

.

На все вычисления с -той степенью параллелизма потребуется () элементарных вычислительных интервалов, а на всем параллельном алгоритме длительностью  их окажется ().

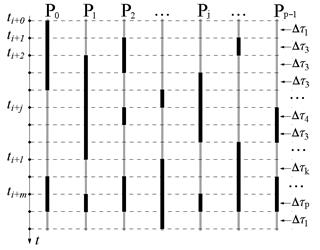Рисунок 1.3.

Относительную долю вычислительных интервалов со степенью параллелизма , в общем их числе во всем алгоритме, обозначим через

.                                                                                  (1.2)

В идеале, на вычисление всех процессов, размещаемых в параллельном алгоритме на  процессорах, один процессор потратил бы время, равное . Взяв число процессоров, равное , в идеальном случае, мы смогли бы выполнить вычисление всех процессов за время в  раз меньшее, чем , т.е. за время, равное ().

Учитывая сказанное, суммарное время выполнения параллельного алгоритма, которое включает интервалы выполнения с различной степенью параллелизма, можно выразить так:

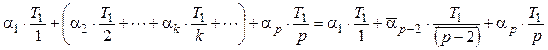
где      – относительная доля вычислительных интервалов со

степенями параллелизма от 2 до ;

            – средняя степень параллелизма для интервалов

параллельного алгоритма со степенями параллелизма от 2 до .

Таким образом, формальную модель ускорения параллельного алгоритма можно записать в следующем, удобном для исследования  виде:

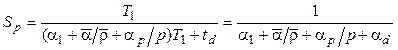,                  (1.3)

где      – доля времени, приходящаяся на пересылку общих

(разделяемых) данных и/или ожидание их готовности.

Рассмотрим несколько поучительных случаев:

1)  . Здесь , что соответствует максимальному ускорению при работе  процессоров по одной и той же программе с разными данными, но без взаимодействия друг с другом.

2)  .  Здесь . Ускорение равно или не превышает средней степени параллелизма.