![]() .
.
Обычный прием ускорения вычислений для этого случая состоит в использовании процедуры сдваивания, то есть замена предыдущего оператора оператором
![]() ,
,
что было рассмотрено ранее (2.2.2).
– Скаляр
® вектор: (![]() ) – некоторый набор скалярных данных x перерабатывается по определенным правилам в массив, элементы которого
зависят от параметра цикла i. Отличие от цикла
скаляр-скаляр в том, что вычисляется не только окончательное значение x, но и сохраняются все его промежуточные значения в виде массива.
Конструкция оператора в этом случае принимает следующий вид:
) – некоторый набор скалярных данных x перерабатывается по определенным правилам в массив, элементы которого
зависят от параметра цикла i. Отличие от цикла
скаляр-скаляр в том, что вычисляется не только окончательное значение x, но и сохраняются все его промежуточные значения в виде массива.
Конструкция оператора в этом случае принимает следующий вид:
![]() .
.
Примером может служить процедура генерирования случайного вектора заданной длины на основе датчика псевдослучайных чисел, в котором очередное число вычисляется по значению предыдущего числа.
– Вектор
® скаляр: (![]() ) – Здесь массивная переменная (вектор,
матрица) посредством определенных правил преобразования (редукции) приводится к
простой переменной. Примерами таких вычислений являются процедуры рекурсивного
сдваивания, которые образуются на выражениях, допускающих равноформатные
ассоциативные разбиения. Это всевозможного рода свертки: проверка кода на четность,
вычисление нормы вектора и прочее, что описано в разделе 2.2.4. Конструкции
этого типа реализуются параллельно, представляя структуру с глубиной,
пропорциональной двоичному логарифму размерности вектора данных.
) – Здесь массивная переменная (вектор,
матрица) посредством определенных правил преобразования (редукции) приводится к
простой переменной. Примерами таких вычислений являются процедуры рекурсивного
сдваивания, которые образуются на выражениях, допускающих равноформатные
ассоциативные разбиения. Это всевозможного рода свертки: проверка кода на четность,
вычисление нормы вектора и прочее, что описано в разделе 2.2.4. Конструкции
этого типа реализуются параллельно, представляя структуру с глубиной,
пропорциональной двоичному логарифму размерности вектора данных.
– Вектор
® вектор: (![]() ) – В циклических вычислениях этого типа
элементы одного вектора (массива, матрицы) преобразуются в элементы другого
вектора (массива, матрицы). Преобразования этого вида являются преобладающими в
задачах, связанных с решениями систем алгебраических уравнений, систем
неравенств, уравнений в частных производных, использующих метод сеток и метод
конечных элементов, и многих других подобных задач в векторно-матричном
представлении. В таких вычислениях параллельность и ускорение могут быть
существенно улучшены за счет различных эвристических приемов преобразования
операторов цикла. Знание информационных особенностей обработки данных позволяет
в некоторых случаях и эти задачи сводить к логарифмической глубине.
Поучительным примером может служить алгоритм упорядочения элементов одномерного
массива x размера n
путем вычисления позиции
) – В циклических вычислениях этого типа
элементы одного вектора (массива, матрицы) преобразуются в элементы другого
вектора (массива, матрицы). Преобразования этого вида являются преобладающими в
задачах, связанных с решениями систем алгебраических уравнений, систем
неравенств, уравнений в частных производных, использующих метод сеток и метод
конечных элементов, и многих других подобных задач в векторно-матричном
представлении. В таких вычислениях параллельность и ускорение могут быть
существенно улучшены за счет различных эвристических приемов преобразования
операторов цикла. Знание информационных особенностей обработки данных позволяет
в некоторых случаях и эти задачи сводить к логарифмической глубине.
Поучительным примером может служить алгоритм упорядочения элементов одномерного
массива x размера n
путем вычисления позиции ![]() i-того элемента в упорядоченном массиве:
i-того элемента в упорядоченном массиве:
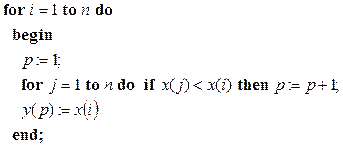 (2.19)
(2.19)
В этом фрагменте на каждое значение индекса i подсчитывается число элементов в массиве, значения которых меньше значения элемента на i-том месте. Полученное число позволяет переписать i-тый элемент на нужное место в упорядоченный по возрастанию выходной массив y.
Для выполнения этой процедуры упорядочения на одном процессоре необходимо время, пропорциональное n2. Знание метода вычисления позиции, который представляет собой условное накопление единиц, независимое от места расположения элементов в исходном массиве, позволяет такое суммирование выполнять одновременно на n процессорах – по процессору на каждый элемент. В свою очередь условное суммирование n единиц выполняется методом сдваивания за время, пропорциональное log2n.
Параллельную версию рассматриваемого алгоритма упорядочения можно было бы теперь представить следующей языковой конструкцией:
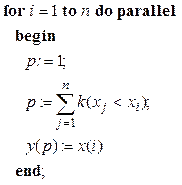 (2.20)
(2.20)
Под знаком суммы стоит символ Кронекера, определяемый здесь, как
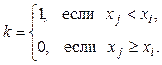
Последний оператор присваивания
требует некоторого времени на пересылку элемента x(i) в упорядоченный массив y
на р-тое место. Из-за этого логарифмическое время упорядочения массива,
наверное, увеличится на время ![]() пересылок
с присваиваниями. Максимальная степень параллелизма, которая при этом будет
достигнута, составит величину
пересылок
с присваиваниями. Максимальная степень параллелизма, которая при этом будет
достигнута, составит величину ![]() .
.
Аппаратурные затраты при максимальной степени параллелизма в этом и подобном ему примере очень велики. Поэтому, в каждом конкретном случае требуется принимать компромиссные решения. В рассмотренном примере, наверное, лучше бы не распараллеливать вычисление условной суммы. Общее время вычислений все равно уменьшилось бы примерно в n раз, а эффективность использования аппаратуры приблизилась бы к 100%.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.