Основой построения параллельного алгоритма может служить как уже существующий последовательный алгоритм, так и сама математическая постановка вычислительной задачи. При распараллеливании существующих последовательных алгоритмов наиболее разумным представляется прагматический подход (от греч. pragmatos – действие), заключающийся в том, что в последовательных алгоритмах находят участки, преобразуемые в параллельные формы, которые и встраиваются в последовательный алгоритм. Такие поиски, преобразования и встраивания в последовательных алгоритмах могут выполняться автоматически. Это открывает возможность использовать на параллельных вычислительных системах программного обеспечения, созданного ранее для однопроцессорных вычислительных машин.
Второй подход, начинающийся с математической подготовки задачи, опирается, в первую очередь, на представление всех этапов преобразования данных в виде ярусной параллельной формы, которая затем формальными или эвристическими методами преобразуется во взаимодействующие ветви процессов, располагаемых и параллельно исполняемых на разных вычислительных машинах.
Для программирования вычислений в параллельных средах необходим параллельный тип мышления. Необходимо уметь мысленно представлять асинхронные процессы своей задачи одновременно в двух измерениях: в пространстве и во времени. Многолетняя практика программирования задач, представляемых лишь одним процессом, изменяющимся во времени, приводит к тому, что эвристические подходы распараллеливания приводят к далеко не лучшим параллельным формам алгоритмов.
К часто встречающимся фрагментам в последовательных алгоритмах можно отнести, например, так называемые альтернированные выражения:
, (2.1)
где 
– чередующиеся
операции 
и 
,
которые
удовлетворяют аксиомам операций сложения и умножения;
– имена операндов,
участвующих в вычислении.
Альтернированное выражение
называют аддитивным, если 
является сложением, и
мультипликативным, если является умножением.
Например, широко известным альтернированным мультипликативным выражением является обобщенная схема Горнера для вычисления значений степенных многочленов:
.
В общем случае, как операции, так и операнды могут быть различной природы. Важно то, что вычисления здесь происходят слева направо путем установки в вычислителе очередной операции и вызова очередного операнда.
Два выражения 
и 
называются
эквивалентными (
) в том и только в том
случае, если, используя конечное число раз законы ассоциативности,
дистрибутивности и коммутативности, можно преобразовать
в и наоборот.
Здесь уместно напомнить, что алгоритмы арифметических выражений, построенные на основе сведения к параллельным эквивалентным арифметическим выражениям, при вычислениях с плавающей точкой не подчиняются закону ассоциативности. Поэтому переход к параллельным вычислительным алгоритмам может привести к увеличению погрешности или к численной неустойчивости эквивалентных им последовательных алгоритмов.
Переход к эквивалентным арифметическим выражениям особенно удобен при разработке специализированных вычислительных микросхем или узлов, в которых благодаря этому можно получить ярусную форму минимальной глубины. При одинаковой длительности всех промежуточных операций это может существенно сократить полное время вычислений узла.
Рассмотрим в качестве примера
несколько алгоритмов вычисления одного и того же арифметического выражения,
применяя двуместные операции 
и 
. Различные алгоритмы зададим скобочными
формами, глубина вложений которых будет характеризовать ярус вычислений.
Алгебраическое выражение
с помощью законов ассоциативности, дистрибутивности и коммутативности преобразуем в следующие эквивалентные формы:
a) 
;
b) 
;
c) 
;
d) 
.
На рисунке 2.2 для каждого выражения приведены
ярусные формы алгоритмов с различными параметрами: числом ярусов 
, числом операций 
и
числом процессоров 
.
 |
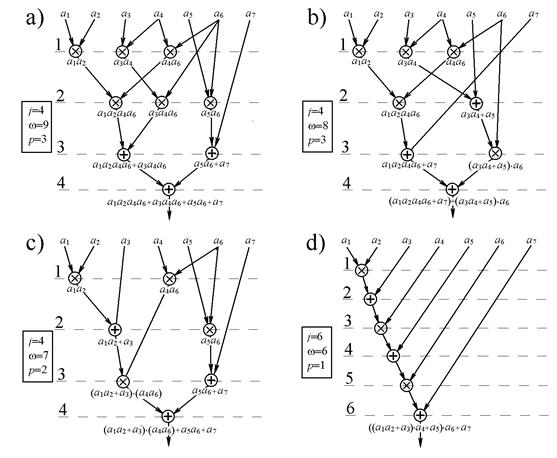Рисунок 2.2.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.