Для модели Винера нечетные коэффициенты имеют такую же функцию как и для модели Гомерштейна. Знаковых функций достаточно, чтобы определить структуру линейной модели и модели Гомерштейна. Дополнительные характеристики: логарифмические наклоны Модель Винера: b3(w0,-t)=a3k3(w0) cos{w0t+U(w0)} –нормированные характеристики;
Используя знаковые функции и критерии можно определить какую модель мы будем иметь, а также определить ее структуру и вид.
Рассмотрим структурную идентификацию, когда имеет запаздывающий элемент.
![]() n>m ; Звено идеального запаздывания – это единственное
звено, которое можно переносить по структуре линейной динамической модели.
n>m ; Звено идеального запаздывания – это единственное
звено, которое можно переносить по структуре линейной динамической модели.
![]()
![]()
![]()
![]()
![]()
1-е условие 2-e условие (**)
При этих сдвигах не будет достигаться min и max логарифмические наклоны, если будет выполняться 1-,2- условия; max DLi и min DLi -нужно найти;
Сначала определяются информационные функции при условиях (**), определяются границы полосы пропускания, фиксируется одна частота, т.е. они подаются на нелинейные динамические объекты и варьируется величина t. При этом используются две измерительные схемы:
1 схема: входной сигнал задерживается во времени;
2 схема: выходной сигнал задерживается во времени;
По уравнениям (**) определяется величина tз , а по функциям max DLi и min DLi – определяют знаковые функции, а затем по ним определяются структурные модели.
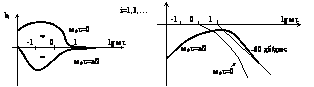 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.