Ответы на экзаменационные вопросы (теория информации, линейные системы), страница 18

МЕТОД РАФЧХ

Этот метод базируется на:

-  использовании в качестве критерия, определяющего качество переходного процесса – ПП регулирования – степень затухания y;

     -      определении РАФЧХ объекта и регулятора

-  применении основного условия устойчивости замкнутой системы.

Степень затухания – величина, характ-щая затухание ПП рег-ния, равная отношению разности двух соседних амплитуд колебания к первой из них: .

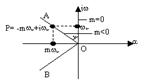
Степень колебательности ПП – характеризует затухание его колебат-ных составляющихщих процесса рег-ния и равна отношению абсолютного значения действительной части к к-ту при мнимой части корня характеристического ур-ния с наименьшим абсолютным значением этого отношения: , р= -a+jw, где a=mw. Получаем, что р_i = -mw+jw. Наложенное на корень ограничение интерпретируется так: степень затухания рассматриваемой составл-щей процесса опред-ся значением: m=tgg; если этот корень харак-го ур-ния будет лежать в плоскости комплексного переменного на линии АОВ, то степень затухания будет одна и та же. Частотные выражения ПФ W(p) звеньев или системы рег-ния, для которых р нах-ся на линии АОВ, наз-ся РАФЧХ и обозначаются W(m, jw).

Исходным условием при расчете оптимальных пар-ров настройки является соотношение:

16. Аппроксимация переходных характерист.

Существует три метода аппроксимации переходных характеристик:

1.  Аппроксимация переходной характеристики объекта апериодическим звеном 1^го порядка.

2. Аппроксимация переходной характеристики объекта апериодическим звеном 2^го порядка (метод Ольденбурга-Сарториуса).

3.Расчет передаточной функции методом интегральных площадей.

Рассмотрим наиболее применяемый метод. Расчет производится в следующей последовательности:

a)  Выделяем на экспериментальной кривой участок чистого запаздывания.

b)  Выбираем  Dt интервала разбиения кривой. Значение интервала разбиения определяется, исходя из условия, что на протяжении всего графика функция h(t) в пределах 2Dt мало отличается от прямой.

c)  Строим переходную характеристику в безразмерном виде, где С(t)=T(Dt)/T_max(t). Для этого значение T(Dt) делим на T_max(t). Получившиеся значения С(t) заносим в таблицу . По данным этого столбика заполняем столбец (1-C) таблицы  и подсчитываем ее сумму.

d)  Определяем площадь F1 по формуле: F1 = Dt*(S(1-C(iDt))-0.5(1-C(0))

e)  Заполняем столбец Q , (1-Q) и (1-Q)(1-С), где Q – безразмерное время.

Q=t/F1            S=(1-С(iDt))*(1-Q_i)

f)  Заполняем столбец 1-2Q+Q²/2 и (1-2Q+Q²/2)(1-С)

S(1-С(iDt))*(1-2Q_i+Q_i²/2)

g)  Определяем интегральные площади:

F2 = DQ*[S(1-C(iDt))*(1-Q_i)-0.5(1C(0))]*F1²

F3=DQ*[S(1-С(iDt))*(1-2Q_i+Q_i²/2)-0.5(1-C(0))]*F1³

h)  Выбираем структуру ПФ. Т.к. в момент времени t=0, h(0)=h¢(0)=h²(0)=0, то выбираем ПФ вида:

W(P)=Kе^-tр/(a3p³+a2p²+a1p+1),

где   a1=F1;  а2=F2;  а3=F3

          К=T(¥)/  x_вх

Если значения F_i < 0, то передаточная функция упрощается.

Таблица

t	T(t)	C=T(t)/Tmax	1-C	F1	Q=t/F1	1-Q	(1-C)(1-Q)	1-2Q+Q^2/2	(1-2Q+Q^2/2)(1-C)	F2	F3