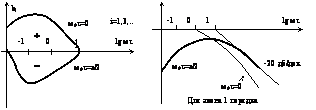Ответы на экзаменационные вопросы (теория информации, линейные системы), страница 39

b_i(w₀, ±t) =kw₀ cos{j (w)};w₀t=0+2kp; w₀t=p/2 +2kp; 2w₀t=p/2;Зависимость не от частоты, а от фазы. Если знаковые функции одинаковые, то можно о модели сказать, что это модель Гомерштейна. Отставание по фазе(4,5,6): на -p/2; на –p;  на  p/2; Примеры знаковых функций:

В основу этого метода положен простой принцип:

Для модели Гомерштейна минимальные (min) логарифмические наклоны одинаковы и поэтому эти модели можно считать (условно) линейными.

Знаковые функции для модели Винера

35. Структурная идентификация линейных динамических систем, основанная на использовании гармонических тестовых сигналов (корреляционный метод).

Получим основные математические уравнения, позволяющие разработать корреляционные методы идентификации со структурами Гомерштейна, Винера и Винера - Гомерштейна.

Входной сигнал модели Гомерштейна дается оператором:

Где y₀ ,g(t) и h(q) определимы в формулах (1) и (2);

Общий оператор описывающий модели Гомерштейна, Винера и Винера – Гомерштейна, имеет вид:

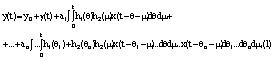
Где x(t)- сигнал на входе, y(t)- сигнал на выходе; g(t)-стационарный шум, независимый от x(t) и имеющий нулевое математическое ожидание; Y₀- постоянная составляющая;

Если в (1) положить и (-обобщенная функция Дирака), то общая модель (1) переходит в частный случай- функциональный оператор модели Гомерштейна.

Если принять h1(q)=d(q) и  h₂(m)=d(m) ,получим модель Винера:

Сигнал определяется соотношением:

Сигнал v(t) недоступен для изменений, используя (*) и (**), получаем следующие интегральные уравнения для импульсных характеристик:

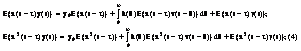
Где E - символ математического ожидания.

При идентификации будут также использоваться следующие интегральные уравнения:

Интегральные уравнения (4) получаются при задержке выходного сигнала во времени, а (5)- входного сигнала.

Входные тестовые сигналы, используемые при идентификации стационарны и эргодичны. Сигнал x(t) не зависит от шума.

36. Непараметрическая и параметрическая идентификация линейных диагностических систем, основанная на использовании гармонических тестовых сигналов (корреляционный метод)

При непараметрической идентификации определяются численные значения импульсных характеристик модулей коэффициентов передачи линейных звеньев и фазовых характеристик. Параметрическая идентификация предполагает определение параметров импульсных моделей, если аналитические выражения для них известны. К таким параметрам, например, относятся постоянные времени линейных звеньев.

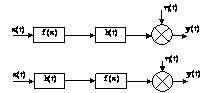
Имеется модель: модель Гамерштейна

 (1)

модель Винера

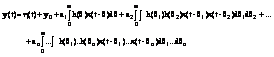 (2)

y – постоянный коэффициент; h – импульсная переходная характеристика линейной динамической части; h -  стационарный шум; а_i – коэффициент безинерционного звена i = 1…n.

Предполагается, что одна из этих моделей адекватно описывает объект.

Постановка задачи:

1.  Необходимо из множества модели (1) и (2) выбрать такую, которая бы адекватно описывала объект.