Ответы на экзаменационные вопросы (теория информации, линейные системы), страница 19

Если переходная кривая харк-ся наличием транспортного запаздывания, то порядок расчета в этом случае следующий:

1.  опред-ем по графику заданной кривой запаздывание t как время в течение которого ф-ция h(t) от t=0 до t=t не превышает 0.001h(¥)/

2.  опред-ем ПФ объекта как произведение 2-х ф-ций: W1(p)=exp(-tp), соответствующей запаздыванию и W2(p), сот-щей ф-ции h(t)=h(t-t), для которой за начало отсчета принято время t=t. Порядок расчета W2(р) изветен, т.к. написан выше. Тогда ПФ объекта запишется так: W(p)=W1(p)*W2(p).

Формулы для определения РАФЧХ:

1. Для объекта W(m,jw)_ОБ = A(m,w)_ОБe ^{–jj(m,w)об}

А(m,w)_ОБ = F_ОБ(w,m,k,T,t)                         j(m,w)_ОБ = Ф_ОБ(w,m,k,T,t)

2. Для регулятора W(m,jw)_РЕГ=A(m,w)_РЕГe ^{–jj(m,w)рег}

А(m,w)_РЕГ = F_РЕГ(w,m,с₀,с₁,с₂)                 j(m,w)_РЕГ = Ф_РЕГ(w,m,с₀,с₁,с₂)

3. Используя условие устойчивости системы W(m,jw)_ОБ* W(m,jw)_Р=1

A(m,w)_РЕГe ^{–jj(m,w)рег} = 1/ {A(m,w)_ОБe ^{–jj(m,w)об}}

Равенство 2^х комплексных чисел возможно в том случае, если равны

модули векторов: A(m,w)_РЕГ = 1/ A(m,w)_ОБ и j(m,w)_РЕГ = –j(m,w)_ОБ

 F_РЕГ(w,m,с₀,с₁,с₂)=1/ F_ОБ(w,m,k,T,t)

 Ф_РЕГ(w,m,с₀,с₁,с₂)=1/ Ф_ОБ(w,m,k,T,t)

4. Решаем систему уравнений c 2^Я неизвестными:

         С₀=f₀(m,w,k,T,t,C₂)                                         C₀=F₁(w,C₂)

         С₁=f₁(m,w,k,T,t,C₂)                                         C₁=F₂(w,C₂)   (*)

5. Если расчет ведут для рег-ра с двумя пар-ми настройки, то палагают, что С₂=0. Если рег-р с тремя пар-ми настройки, то определяют С₀ и С₁ в звис-ти от частоты w для различных С₂.

6. Подставить в ур-ние (*) численное значение частоты от w=0 до w= значению, при котором С₀ становится < 0. Строим график завис-ти С₀=f(С₁). Если рег-р с 3-мя пар-ми, то строят неск-ко завис-тей С₀=f(С₁) для различных С₂, начиная с С₂=0.

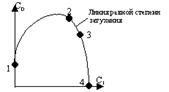
Все С₀ и С₁, лежащие внутри области ограниченной кривой, обеспечивают процесс рег-ния y > y_зад, а лежащие вне области y < y_зад. Если токи на кривой, то y = const(>0). На кривой выбирается нес-ко точек, для каждой из них с помощью ЭВМ(АСОТАР) строим ПП и находим оптимальные настройки. Оптимальным считается процесс, соответствующий точке 2, т.к. статич. ошибка d=0 и длительность ПП будет min. Оптимальные настройки получаются в точках, которые находятся правее линии максимума. Значения настроечных пар-ро, лежащие на пересечении кривой с осью абсцисс, т.е. С₀=0 соответствуют П-рег-ру и характ-ся остаточной неравномерностью (точка 4).  Значения настроечных пар-ро, лежащие на пересечении кривой с осью ординат, т.е. С₁=0 соответствуют И-рег-ру, называемому атстатическим, т.е. без ошибки (точка 1). Выбираем y=0.75-0.9. если y<0.75, то процесс будет недостаточно интенсивный. Если y>0.9, то имеем дело с завышенным отклонением регулируемой величины.